Perspectiva isométrica
Hace tiempo que los juegos dieron el salto al 3D cada vez más juegos, cada vez más realistas. Antes de eso, debíamos conformarnos con simulaciones hechas sobre 2D: me refiero a los juegos a base de mosaicos isométricos. O lo que tradicionalmente se ha llamado isométrico, pues en realidad no lo es y lo veremos en adelante. Los juegos de estrategia de la época utilizaban este tipo de representación para dar la sensación de tener un despliegue de lo que fuera en perspectiva. Hay juegos modernos, que aun siendo verdaderos juegos 3D utilizan una cámara ortográfica situada de manera que proporcionan una sensación equiparable a los juegos tradicionales.
Hoy vengo a cansinar con el tema y traigo algo de código para trastear. Primero veremos un poco sobre perspectivas, aunque no sea de manera exhaustiva, sí me gustaría explicar cuatro tipos de perspectiva1.
Perspectivas
|
|
|
|
|
|
Las vistas en cada perspectiva tratan de representar los objetos de una forma más o menos realista. No hace falta decir que la perspectiva más realista para nuestro ojo es la perspectiva cónica o 3D pura. Sin embargo, el problema de esta representación es que es complicado establecer una escala fácilmente dimensionable. Por eso, en la representación de sólidos más técnica se suelen utilizar aquellas otras representaciones que permiten acomodar una escala para poder medir correctamente las dimensiones del objeto. Es decir, se utilizan las proyecciones ortométricas como las cuatro que vemos arriba.
En la Figura 1 podemos observar una perspectiva oblicua, se llaman así
porque presentan una vista desde un lado, manteniendo la escala fija
en dos ejes. En la figura podemos observar que los ejes y y z se han
colocado a 90°. Ambos mantendrán una escala proporcional a lo largo de
todo el eje. El oblicuo x se representa con una escala proporcional.
En este caso, se presenta a 135° con respecto a los otros dos, pero
también pueden utilizarse ángulos múltiplos de 30° y 45°, dejando de
lado los 90°, 180°, 270° y 360° (por razones obvias). La escala de
reducción en el eje x dependerá también del ángulo seleccionado, los
valores habituales son 1:2, 2:3 ó 3:4.
La ventaja de la perspectiva isométrica (Figura 2) es que al repartir el espacio en tres ángulos de manera equitativa (120º), todos los desplazamientos en cualquiera de los ejes tiene la misma escala. Este tipo de proyección es bastante utilizada en representaciones de instalaciones de fontanería, de gas, eléctricas, donde se puede representar toda la habitación a escala. Tradicionalmente ha dado nombre a la representación gráfica de algunos juegos donde se simula un mundo 3D en la pantalla.
Sin embargo, la realidad es que este tipo de juegos utilizan una
perspectiva dimétrica (Figura 3). En general, esta perspectiva
mantiene equivalente la escala en dos ejes, teniendo un factor de
reducción para el tercero. La utilización de este tipo de perspectiva
en los videojuegos es por una razón de cálculo y vistosidad. Los
ángulos que se muestran en la figura pueden variar, sin embargo,
manteniendo esos que aparecen en la figura, tenemos un desplazamiento
en horizontal que es el doble del desplazamiento en vertical. Es
decir, desplazarse en x o en y sobre la pantalla mantiene una
proporción de 2:1. En pantalla, por cada pixel que se avance en
vertical, se deberán avanzar dos en horizontal para un desplazamiento
equivalente. Para los cálculos también es una escala adecuada: todos
sabemos lo rápido que es para un ordenador (binario) multiplicar o
dividir por 2.
Por último, el la Figura 4 se representa una perspectiva en la que los tres ejes mantienen proporciones distintas y por lo tanto hay que aplicarle a cada uno su factor de reducción correspondiente.
Texturas y píxeles
Para no perder mucho tiempo haciendo texturas para las pruebas, he hecho algunas muy básicas, aunque también podría haber descargado un paquete de texturas ya hecho, he preferido hacerlo yo todo. Para ello he utilizado como editor Krita, que cada vez que lo abro me gusta más y prácticamente me ha hecho replantearme el desinstalar Gimp.
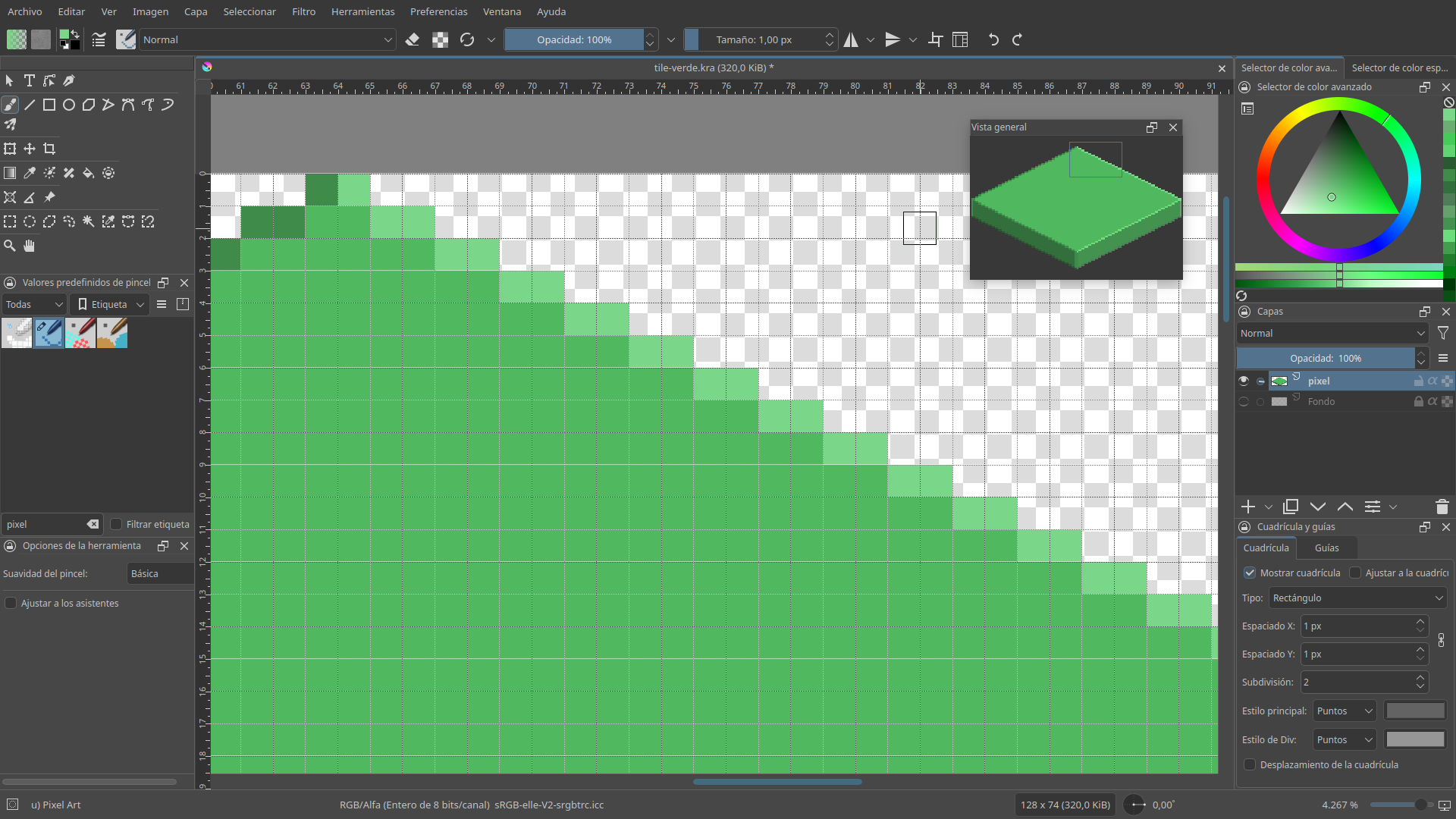
He creado dos teselas básicas, una verde y otra ocre, para hacer las pruebas. Sobre las dimensiones básicas de 128 \(\times\) 64 he añadido 10 de alto, para dar un poco de profundidad.
Además, en los laterales he dejado a propósito un píxel de margen por cada lado, para que al dibujarlos los límites de cada tesela sean más evidentes. En muchos juegos se intenta eliminar ese efecto de rombos para mejorar la sensación de continuidad del mundo, pero en este caso prefiero mostrar las separaciones de manera didáctica.
Antes de nada comenzaremos con una representación de texturas en un mundo plano con vista cenital.
Sobre los ejes
En un mundo plano, en 2D, hacer coincidir los puntos del mundo virtual
con los puntos de la pantalla, pasa por un simple cambio de
coordenadas. Debemos cambiar el origen y también el signo o sentido
de los desplazamientos en el eje y. Sin embargo, las direcciones
seguirán siendo las mismas: horizontal y vertical. Por tanto, la
representación de algo 2D en pantalla es sencillo.
En los sistemas de coordenadas cartesianas podemos representar puntos
del plano mediante el eje horizontal x, que crece hacia la derecha y
decrece hacia la izquierda, y el eje y, que crece hacia arriba y
decrece hacia abajo. Este sistema permite representar también con
coordenadas negativas. Por otro lado, en la pantalla del ordenador,
los puntos vienen representados por coordenadas siempre positivas, que
en x crecen en horizontal hacia la derecha, como en las cartesianas,
pero en vertical, en y, crecen hacia abajo, al contrario que en las
cartesianas.
Si dibujamos un mosaico cuadrado, donde cada tesela tenga un lado de, digamos, 64 píxeles, las coordenadas de pantalla se pueden calcular de manera fácil a partir de las coordenadas de las teselas.
Por ejemplo, para saber dónde debe iniciarse el dibujo de la tesela
(3, 2), basta multiplicar cada valor, por el ancho de la textura, –en
nuestro ejemplo 64–, de manera que debemos colocar la imagen a partir
del punto (192, 128) o expresado como:
\[x_p = x_t \times w_t\] \[y_p = y_t \times h_t\]
donde:
- \(x_p\) es la coordenada
xen pantalla. - \(x_t\) es la coordenada
xde la tesela. - \(y_p\) es la coordenada
yen pantalla. - \(y_t\) es la coordenada
yde la tesela. - \(w_t\) es el ancho de la tesela, y
- \(h_t\) es el alto de la tesela.
Un mosaico de este tipo tiene la utilidad de servir de fondo para dibujar encima de él otras texturas, sprites o animaciones. Para ello es bastante habitual que necesitemos conocer otras posiciones o desplazamientos en la pantalla, una de las más frecuentes es su punto medio. Si queremos saber cuál es el punto medio de una tesela, el cálculo será el siguiente:
\[x_p = x_t \cdot w_t + \frac{w_t}{2}\] \[y_p = y_t \cdot h_t + \frac{h_t}{2}\]
donde:
- \(x_p\) es la coordenada
xen pantalla. - \(x_t\) es la coordenada
xde la tesela. - \(y_p\) es la coordenada
yen pantalla. - \(y_t\) es la coordenada
yde la tesela. - \(w_t\) es el ancho de la tesela, y
- \(h_t\) es el alto de la tesela.
El orden natural de dibujo es de izquierda a derecha y de arriba hacia
abajo. Por lo que podemos crear una matriz de teselas con la
información de qué textura debo cargar en cada una de ellas y con un
bucle anidado para x dentro de un bucle para y, se dibujarán todas en
el orden correcto.
Por ejemplo, utilizando löve2D podemos hacer una prueba rápida. Dejo también el código para que lo podáis descargar de la página, lo encontraréis el enlace más abajo al final del apartado de Otras consideraciones.
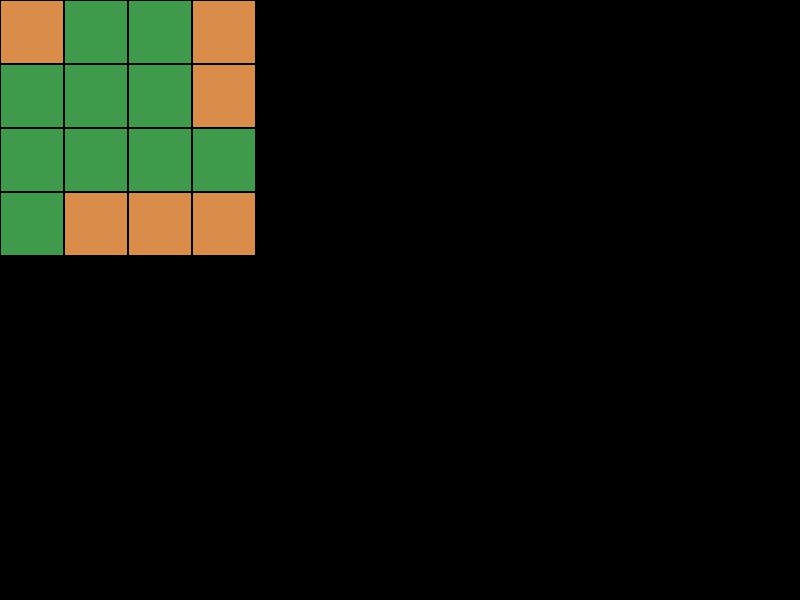
Todos esos cálculos sencillos son algo más complejos cuando se trata de echar una mirada a cómo resulta la misma matriz desde la perspectiva isométrica. Veamos primero un esquema y haré consideraciones a partir de esta gráfica:
El punto (0, 0) ya no se encuentra en la esquina superior izquierda,
como en el modelo anterior, sino arriba, ni siquiera en el centro,
sino desplazada hacia la izquierda. ¿Cuánto? la mitad del ancho de la
tesela multiplicado por el número de filas menos uno. Por expresarlo,
matemáticamente:
\[ x_p = (filas - 1) \times \frac{w_t}{2} \]
donde:
- \(x_p\) es la coordenada
xen pantalla - \(filas\) es el número de filas del mosaico
- \(w_t\) es el ancho de nuestra tesela.
Es decir, la posición horizontal de una tesela, también depende del
eje y del mosaico y de la mitad del ancho de cada tesela ( \(w_t/2\)
). Expresado de otra manera: según se avanza la fila, para una misma
columna, la coordenada x en pantalla disminuye medio ancho de tesela
por cada fila.
Para dibujar el resto, a partir de ese punto inicial, si nos fijamos
en el esquema de la figura 10, podemos comprobar que la siguiente
tesela, la (1,0) se encuentra situada con un desplazamiento de medio
ancho de la textura hacia la derecha y medio alto de la textura hacia
abajo. La posición general en x será:
\[ x_p = x_{inicio} + \frac{w_t}{2} \] \[ y_p = y_{inicio} + \frac{h_t}{2} \]
donde:
- \(x_p\) es la coordenada
xen pantalla - \(y_p\) es la coordenada
yen pantalla - \(x_{inicio}\) es la coordenada
xdonde empezamos a dibujar - \(y_{inicio}\) es la coordenada
ydonde comenzamos a dibujar - \(w_t\) es el ancho de nuestra tesela y
- \(h_t\) es el alto de la tesela.
Para el punto (2,0) nos encontramos que la fórmula quedaría:
\[ x_p = x_{inicio} + 2 \times \frac{w_t}{2} \] \[ y_p = y_{inicio} + 2 \times \frac{h_t}{2} \]
y para el punto (3, 0) será:
\[ x_p = x_{inicio} + 3 \times \frac{w_t}{2} \] \[ y_p = y_{inicio} + 3 \times \frac{h_t}{2} \]
Podríamos concluir que para la primera fila, cuya coordenada en el
mosaico es 0, la fórmula general sería:
\[ x_p = x_{inicio} + x \times \frac{w_t}{2} \] \[ y_p = y_{inicio} + x \times \frac{h_t}{2} \]
donde:
- \(x_p\) es la coordenada
xen pantalla - \(y_p\) es la coordenada
yen pantalla - \(x_{inicio}\) es la coordenada
xdonde empezamos a dibujar - \(y_{inicio}\) es la coordenada
ydonde comenzamos a dibujar - \(x\) es el valor de la columna en el mosaico
- \(w_t\) es el ancho de nuestra tesela y
En la fórmula anterior falta algo, ya habíamos visto que para la
primera columna, los valores de x disminuían. Si nos centramos en las
coordenadas de la primera tesela de la siguiente fila, el cálculo será
distinto. Para empezar, el valor de \(x_p\) disminuye, según observamos
en la Figura 10. Concretamente, las coordenadas de la tesela (0,1)
son:
\[ x_p = x_{inicio} - \frac{w_t}{2} \] \[ y_p = y_{inicio} + \frac{h_t}{2} \]
donde:
- \(x_p\) es la coordenada
xen pantalla - \(y_p\) es la coordenada
yen pantalla - \(x_{inicio}\) es la coordenada
xdonde empezamos a dibujar - \(y_{inicio}\) es la coordenada
ydonde comenzamos a dibujar - \(w_t\) es el ancho de nuestra tesela y
- \(h_t\) es el alto de la tesela.
Como ya mostré antes, las posiciones disminuirán en su valor x según
aumenten las filas. La fórmula completa será:
\[ x_p = x_{inicio} + x\left(\frac{w_t}{2}\right) - y\left(\frac{w_t}{2}\right) \] \[ y_p = y_{inicio} + x\left(\frac{h_t}{2}\right) + y\left(\frac{h_t}{2}\right) \]
Si sacamos factor común para ahorrarnos una operación de multiplicación:
\[ x_p = x_{inicio} + (x - y) \frac{w_t}{2} \] \[ y_p = y_{inicio} + (x + y) \frac{h_t}{2} \]
Modificando ligeramente el código que ya tenemos hecho, podemos
convertir el dibujo del mosaico plano en su representación
isométrica2. Concretamente, para ahorrar cálculos, se han
declarado las variables globales Wt2 que representa la mitad del ancho
de la tesela y Ht2 que representa la mitad del alto de la
tesela. Además se declaran también las variables x_inicio e
y_inicio. En el mundo plano no hacía falta un punto de inicio, porque
se asume que era (0,0). Por supuesto, también cambian las imágenes de
las teselas:
local x_inicio = Wt2 * (ANCHO_MALLA - 1) local y_inicio = 0
Por supuesto, también se ha modificado el código para dibujar una tesela:
-- Dibujar la tesela function dibuja_tesela(imagen, x, y) local xp = x_inicio + (x - y) * Wt2 local yp = y_inicio + (x + y) * Ht2 love.graphics.draw(IMAGENES[imagen], xp, yp) end
Un pantallazo confirma que todo marcha según lo esperado:

Otras consideraciones
Esta es la versión muy simplificada de cómo dibujar mosaicos
«isométricos» en juegos 2D. Podemos complicar un poco más las cosas y
trabajar también en el eje z o para detectar el cursor:
La detección del cursor implica otro poco de cálculo. Disculpad si no me alargo con las explicaciones de esta fórmula, seguro que encontráis por internet explicaciones mejores que la mía. El código añadido para manejar el cursor es el siguiente:
-- Detectar ratón function detecta_raton() -- obtener las coordenadas del cursor local xr = love.mouse.getX() local yr = love.mouse.getY() -- convertir las coordenadas de pantalla a tesela local xt = math.floor((yr / Ht) + (xr / Wt)) - 2 local yt = math.floor((yr / Ht) - (xr / Wt)) + 2 -- dibujar la textura de tesela seleccionada dibuja_tesela(tesela_cursor, xt, yt) end
Después en la función love.draw() se añade una llamada a esta función
al final, tras haber dibujado el mosaico.
Lo único que puedo aconsejaros es que juguéis un poco, si queréis profundizar. Instalar Löve2D y retorcer el código fuente junto con las imágenes utilizadas, que podéis encontrar en este archivo. Quizá incluso decidiros a hacer un pequeño proyecto a partir de esa base. O si preferís otro lenguaje u os da pereza el instalar Lua y Löve, el código es tan sencillo que seguro podéis adaptarlo a cualquier otra herramienta o lenguaje.
Descargar fuentes pinchando aquí → perspectivas.zip


Comentarios