Cámara

Reorganización del código
Desde la última entrega de la serie he modificado algunas cosas del
pequeño raytracer. Hasta ahora venía lanzando procesos
independientes para imagen y camara, haciéndolo por
separado desde el lanzador que había metido con calzador en la
librería general del raytracer.
Lo que he hecho es utilizar sólamente el proceso camara desde la
definición de la escena y que sea éste proceso el que levante los
otros procesos auxiliares como imagen o renderer. Así pues, en el
fichero de escena, a partir de ahora, sólo encontraremos los
parámetros de configuración de la imagen, la cámara y los
objetos1 del mundo.
El formato ppm
Además, en los últimos días he cambiado el formato de salida. Hasta
ahora venía guardándose el fichero ppm como P3 (ASCII) al formato
binario P6. Es básicamente lo mismo, pero ocupa bastante menos y se
escribe bastante más rápido.
Explico un poco más cómo funciona ésto del formato ppm porque hay
quien ha mostrado curiosidad por él y por qué lo utiliza el libro. No
estoy seguro de saber por qué lo usa el autor, sin embargo parece ser
el formato mejor pensado, quizá, para ser entendido por humanos. Por
otro lado, debería referirme a dicho formato como PNM o Portable
Anymap Format, que engloba a varios tipos de fichero cada uno con su
extensión:
| Tipo | ASCII | raw | Ext. | Colores |
|---|---|---|---|---|
| Portable Bitmap | P1 | P4 | .pbm | 0-1 (Blanco y Negro) |
| Portable Graymap | P2 | P5 | .pgm | 0-255 y 0-65535 (Escala de Grises) |
| Portable Pixmap | P3 | P6 | .ppm | 0-255 por cada canal: R,G,B.2 |
Estos ficheros cuentan con una cabecera en ASCII con el tipo de fichero seguido con hasta tres valores numéricos y separado de los datos por un salto de línea:
| Cabecera | Significado |
|---|---|
| P1..P6 | Tipo de fichero |
| "#" | Comentario encabezado por # |
| 1 | Ancho de la imagen |
| 2 | Alto de la imagen |
| 3 | Valor máximo del pixel |
| "\n" | Separación de cabecera y datos |
Estos valores no tienen por qué estar escritos uno en cada línea. El único valor que debe estar en una línea es el comentario, en el caso de que lo haya.
Por poner un ejemplo de cómo se ve un fichero ASCII:
P2 # Shows the word "FEEP" (example from Netpbm man page on PGM) 24 7 15 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 3 3 3 0 0 7 7 7 7 0 0 11 11 11 11 0 0 15 15 15 15 0 0 3 0 0 0 0 0 7 0 0 0 0 0 11 0 0 0 0 0 15 0 0 15 0 0 3 3 3 0 0 0 7 7 7 0 0 0 11 11 11 0 0 0 15 15 15 15 0 0 3 0 0 0 0 0 7 0 0 0 0 0 11 0 0 0 0 0 15 0 0 0 0 0 3 0 0 0 0 0 7 7 7 7 0 0 11 11 11 11 0 0 15 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

Estos son los formatos básicos. Hay otro que se marca con P7 que
permite la utilización del canal transparente. Dicho de otro modo, su
modelo de color es RGBA. Nos referimos a este tipo, para englobarlo
con los anteriores como PAM (Portable Arbitrary Map).
| Cabecera | Valor | Significado |
|---|---|---|
| P7 | número mágico | |
| WIDTH | Número | ancho de la imagen |
| HEIGHT | Número | alto de la imagen |
| DEPHT | Número | profundidad de color |
| MAXVAL | Número | valor máximo |
| TUPLTYPE | Cadena | tipo de imagen |
| ENDHDR | Final de la cabecera |
La mayoría de estos valores no necesitan explicación, sin embargo,
TUPLTYPE implica algunas consideraciones más. Este formato no tiene
versión ASCII legible por humanos y puede englobar a todos los
formatos anteriores según el valor de ese parámetro:
| TUPLTYPE | MAXVAL | DEPTH | Comentario |
|---|---|---|---|
| BLACKANDWHITE | 1 | 1 | Equivalente a un pbm tipo P4 |
| GRAYSCALE | 2..65535 | 1 | Equivalente a un pgm tipo P5 |
| RGB | 1..65535 | 3 | Equivalente a un ppm tipo P6 |
| BLACKANDWHITE_ALPHA | 1 | 2 | 2 bytes por pixel |
| GRAYSCALE_ALPHA | 2..65535 | 2 | |
| RGB_ALPHA | 1..65535 | 4 |
En todos los casos, cuando MAXVAL > 255 se utilizan 2 bytes por
canal.
En el raytracer utilizo el formato de fichero P6. La cabecera de
la imagen final que he puesto es: P6 600 400 255, un salto de línea
y luego los datos en binario. La misma cabecera para un fichero en
esta última versión sería:
P7 WIDTH 600 HEIGHT 400 DEPTH 3 MAXVAL 255 TUPLTYPE RGB ENDHDR
A continuación se encontrarían los datos de los pixeles, de la misma
manera que en nuestra imagen P6. La única diferencia entre ambos
fichero serían las respectivas cabeceras.
Como dije antes, venía utilizando el modo P3 como formato de
fichero, pero el que sea legible por humanos no aporta mucho al
fichero más allá de necesitar bastante más espacio para almacenarse.
El tema es que, puesto que no vamos a hacer modificaciones manuales a
la imagen, podemos utilizar su formato raw o binario. Para ello he
modificado el código de escritura del archivo gráfico de la siguiente
manera:
escribir_imagen(#state{ancho=Ancho,alto=Alto,lienzo=Lienzo,fichero=Fichero}) -> Cabecera = io_lib:format("P6 ~p ~p 255~n", [Ancho,Alto]), Imagen = lists:map( fun(J) -> lists:map( fun(I) -> Color = maps:get({I,J},Lienzo,{1,0,1}), escribe_color(Color) end, lists:seq(0, Ancho-1)) end, lists:seq(Alto-1, 0, -1)), {ok, F} = file:open(Fichero, [write]), file:write(F, Cabecera ++ Imagen), file:close(F). escribe_color({R,G,B}) -> [round(255 * rerl:clamp(R, 0.0, 0.9999)), round(255 * rerl:clamp(G, 0.0, 0.9999)), round(255 * rerl:clamp(B, 0.0, 0.9999))].
Como se puede apreciar, lo que ha cambiado es que ya no se convierte
el color a una cadena ASCII, lo demás continúa igual. Salvo que la
función escribe_color/1 ha pasado de la librería rerl a ser parte
del módulo imagen pues sólo se la llama desde allí.
No descarto, en un futuro, modificar la salida al modo P7 y que se
pueda seleccionar el tipo de salida del raytracer desde el blanco y
negro hasta el color completo con, o sin, canal alfa.
Puesto que ya tenemos nuestra cámara generándonos las imágenes en un formato raw3 ahora nos faltan algunos otros detalles para fabricarnos nuestra cámara virtual.
Cámara
El esquema más sencillo de nuestra cámara está representado por un punto en el espacio y un lienzo en el que dibujar:
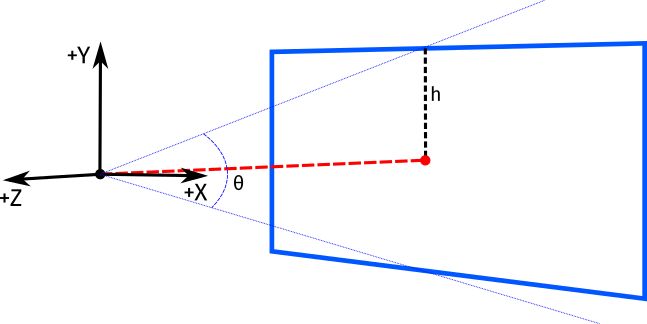
En nuestra cámara podemos observar que el ángulo de visión \(\theta\) es equivalente a \(2h\) y por tanto, para calcular \(h\) podemos hacer \(h=tan(\frac{\theta}{2})\) que más adelante nos hará falta.
De momento, lo que más falta nos hace para representar una cámara independiente es que la podemos mover y apuntar mirando en una dirección determinada, que la podamos inclinar en cualquier dirección del espacio 3D. La alternativa sería dejar la cámara fija y mover el mundo para situarlo frente a ella, que es lo que veníamos haciendo.
Hasta ahora, para resumir un poco lo que era nuestra cámara,
situábamos su origen en el punto {0,0,0}; apuntaba, o miraba, en
la dirección {0,0,-1} y su inclinación era el vector {0,1,0}. Sin
embargo, queremos hacer que nuestra cámara se pueda colocar en
cualquier punto del espacio, mirando a cualquier otro punto del mismo
y poder inclinarla en cualquier dirección. Por tanto, hay que cambiar
el sistema de referencia a algo como:
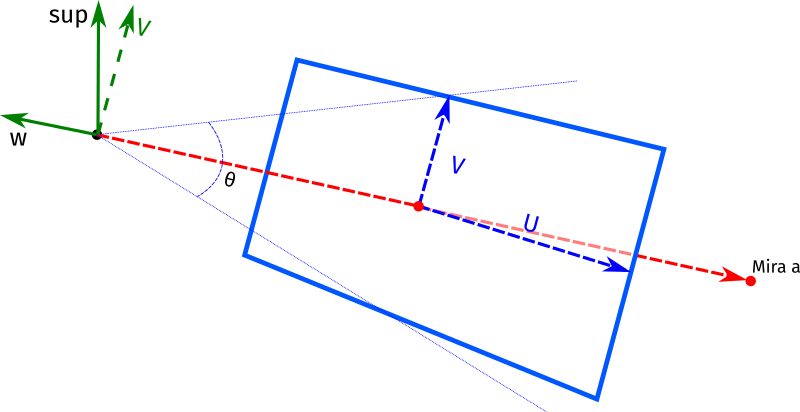
Hay que remarcar que aunque no se aprecie de manera exacta en la
figura tanto Vup como v y w coinciden en el mismo plano. Si el
valor Vup es {0,1,0} el plano al que me refiero será vertical y
nuestra cámara hará unas imágenes horizontales perfectas, pero si lo
inclinamos 45º a la izquierda estableciéndolo a {-1,1,0} obtendremos
una imagen tal que:

Código de la cámara
Muy bonito todo pero ¿cómo ha quedado el código? Ya me perdonaréis si me enrollo y no pongo una sola fórmula ni una sola línea de código. Así que allá va un poco de código. Primero comento que he creado un registro cámara para los valores básicos:
-record(camara, { origen = {0,0,0} % Posición de la cámara , mira = {0,0,-1} % Punto al que mira , sup = {0,1,0} % Orientación , angulo = 80}). % Ángulo del campo de visión
Comentar sólamente que el valor del ángulo por defecto es de 80º para el campo de visión vertical. Como la elección de ese valor por defecto no es aleatoria y necesita un poco más de explicación quiero sólo remarcar el hecho y pedir paciencia, porque el porqué vendrá explicado más adelante.
Para lanzar los rayos que generan la imagen, primero necesitamos el
punto desde el que debemos hacerlo (origen). También necesitamos
saber en qué dirección se encuentra el lienzo (mira), hacia dónde
está mirando la cámara. Por último, también necesitamos saber la
verticalidad de la cámara (arriba).
El registro nos sirve también para poder tener valores por defecto que
funcionan en la mayor parte de los casos. De esta manera en el fichero
de la escena seguramente nos sobre con pasar a la función start de
la cámara, los parámetros que cambien: generalmente, los puntos
origen y mira.
Dicha función queda de la siguiente manera:
start(#camara{origen=Origen,mira=MiraA,sup=VArriba,angulo=CV}, #config{ratio=Ratio,ancho=Ix,muestras=Muestras,profun=Profun,tesela=Tesela,procesos=Procesos}=Config) -> io:format("Estableciendo datos de la imagen...~n"), Pid = rerl_imagen:start(Config), register(imagen, Pid), io:format("Estableciendo datos de la cámara...~n"), Theta = rerl:grados_a_radianes(CV), % Calcular el ángulo en radianes del campo de visión H = math:tan(Theta / 2), Viewport_Alto = 2.0 * H, % Calcular el factor de altura de la imagen Viewport_Ancho = Viewport_Alto * Ratio, W = rerl:vector_unidad(rerl:resta(Origen, MiraA)), U = rerl:vector_unidad(rerl:cruz(VArriba, W)), V = rerl:cruz(W, U), Iy = round(Ix / Ratio), Horizontal = rerl:mul(U, Viewport_Ancho), Vertical = rerl:mul(V, Viewport_Alto), %% Eii = Origen - Viewport_Ancho/2 - Viewport_Alto/2 - {0,0,Focal} Medio_H = rerl:dividir(Horizontal, 2), Medio_V = rerl:dividir(Vertical, 2), Eii = rerl:resta( rerl:resta( rerl:resta(Origen, Medio_H), Medio_V), W), Estado = #state{origen=Origen , alto=Viewport_Alto , ancho=Viewport_Ancho , ix=Ix , iy=Iy , ratio=Ratio , horizontal=Horizontal , vertical=Vertical , eii=Eii , muestras=Muestras , profundidad=Profun , tesela=Tesela , procesos=Procesos}, spawn(rerl_camara, init, [Estado]).
El cambio no es muy pronunciado: como se puede apreciar es que se
calcula U y V en base al ángulo del campo de visión vertical.
La imagen conseguida con un fichero escena tal que:
escena() -> Config = #config{ nombre = "imagen.ppm", % Nombre del fichero de imagen generado ratio = 16 / 9, % Ratio ancho/alto de la imagen ancho = 400, % Ancho en puntos de la imagen muestras = 100, % Nº de muestras por pixel profun = 50, % Número de «rebotes» por rayo. tesela = 25, % Tamaño del lado de la tesela en puntos procesos = 10}, % Número de procesos de cálculo io:format("Iniciando la cámara...~n"), O = {-2,2,1}, % Origen de la cámara MiraA = {0,0,-1}, CV = 90, % Campo de visión vertical (ángulo en grados) Camara = #camara{origen=O,mira=MiraA,angulo=CV}, Pid_camara = rerl_camara:start(Camara, Config), register(camara, Pid_camara), %% Materiales de la escena Material_Suelo = #material{tipo=difuso,albedo={0.2,0.2,0.0}}, Difuso = #material{tipo=difuso,albedo={1.0,0.0,0.0}}, Cristal = #material{tipo=transparente,albedo={1.0,1.0,1.0},ir=1.5}, Metal = #material{tipo=reflexion,albedo={0.8,0.6,0.2},rugoso=0.3}, %% Esferas: geometrías de la escena Esfera_Suelo = #esfera{centro={0,-100.5,-1},radio=100}, Esfera_Central = #esfera{centro={0,0,-1},radio=0.5}, Esfera_Izda = #esfera{centro={-1.0,0.0,-1.0},radio=0.5}, Esfera_Dcha = #esfera{centro={1.0,0.0,-1.0},radio=0.5}, %% Montar los objetos para el render, cada geometría con su material Objs = [#objeto{geom=Esfera_Central,material=Difuso} , #objeto{geom=Esfera_Suelo,material=Material_Suelo} , #objeto{geom=Esfera_Izda,material=Cristal} , #objeto{geom=Esfera_Dcha,material=Metal}], %% Tirar el render camara ! {render,Objs}.
Genera la siguiente imagen:

Sin embargo, si modificamos el ángulo a 20:

Como se puede apreciar a ángulos de visión más estrechos, la imagen se acerca como en un teleobjetivo. Para ángulos grandes la imagen se alejará como en un gran angular. Por ejemplo, con un valor de 160º, que sería casi un angular ojo de pez, la imagen se vería así:

Como observaréis, los grandes angulares distorsionan y curvan los objetos. La esfera inferior aparece con lados casi rectilíneos no como se esperan ver en una esfera.
¿Por qué cambia tanto la imagen cambiando sólo el ángulo del campo de visión? Dejadme un momento que explico un poco mejor cómo funciona una cámara fotográfica.
Cámara fotográfica
Al ojo humano podemos calcularle un ángulo de visión, o campo visual, de 130º en horizontal y 80º en vertical4.
Para los cálculos vamos a fijarnos en el siguiente esquema:
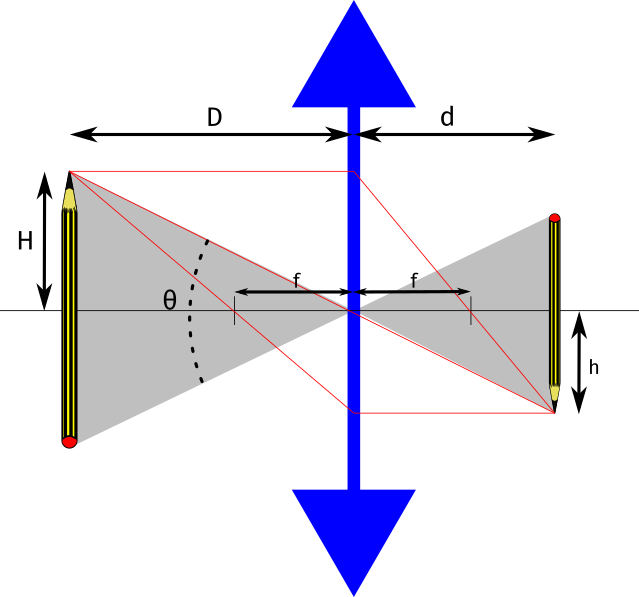
En una lente simple, no hay sensores como en las cámaras para tener como referencia su tamaño, puesto que las distancias focales y cualquier otro parámetro estará calculado en función a él. Resulta un poco difícil explicar, por qué los angulares en la fotografía se miden en mm o por qué decimos que un objetivo de 50mm es el angular normal. Para ello tengo que cansinaros un poco más con las matemáticas.
Vamos a darle un poco al cálculo del ángulo de visión en función de la distancia focal y el tamaño del sensor (el normal es 35mm):
\[ \theta = 2 arctan \frac{S}{2f(m+1)}\]
donde \(\theta\) es el ángulo de visión, \(S\) el tamaño del sensor, \(F\) la distancia focal y \(m\) el factor de magnificación que los aficionados a la fotografía conocerán como macro. Para distancias de enfoque grandes (\(m \thickapprox 0\)) sería:
\[ \theta = 2 arctan \frac{S}{2f}\]
El factor de magnificación, o macro, es despreciable en distancias de enfoque lejanas (al infinito), pero tiene que tomarse en cuenta en distancias de enfoque cercanas. Se calcula mediante la fórmula:
\[m = \frac{f}{D - f}\]
Donde \(f\) es la distancia focal en mm y \(D\) es la distancia de enfoque. Por ejemplo, con un objetivo de 50mm enfocado a una distancia de 55cm el cálculo sería:
\[m = \frac{f}{D - f} = \frac{50}{550 - 50} = 0,1\]
Por eso, entre las recomendaciones habituales que se les da a los fotógrafos noveles cuando te están enseñando fotografía, encuadres y demás, es que te alejes del sujeto al menos un metro para no distorsionar la imagen... pero seguimos.
Por hacer una comparación si calculamos con un objetivo de 50mm su
ángulo de visión para estar enfocado al infinito, puesto que el factor
m es igual a cero (\(m=0\)), dicho ángulo será:
\[\theta = 2 arctan \frac{S}{2f(m+1)} = 2 arctan \frac{36}{2 \cdot 50} = 40º\]
Sin embargo, si lo enfocamos a 55cm como dijimos antes:
\[\theta = 2 arctan \frac{S}{2f(m+1)} = 2 arctan \frac{36}{2 \cdot 50 (0,1 + 1)} = 36º\]
Es decir, el ángulo es cuatro grados menor, no podrás enfocar bien a distancias menores, a no ser que el objetivo sea macro y permita mover las lentes para reducir ese ángulo. Si no es macro, tendrás que cambiar el objetivo y calzarle a la cámara un gran angular.
Enfoque
En una fotografía estamos acostumbrados a ver que hay objetos que vemos borrosos. Aquellos que están demasiado lejos o demasiado cerca del punto enfocado.
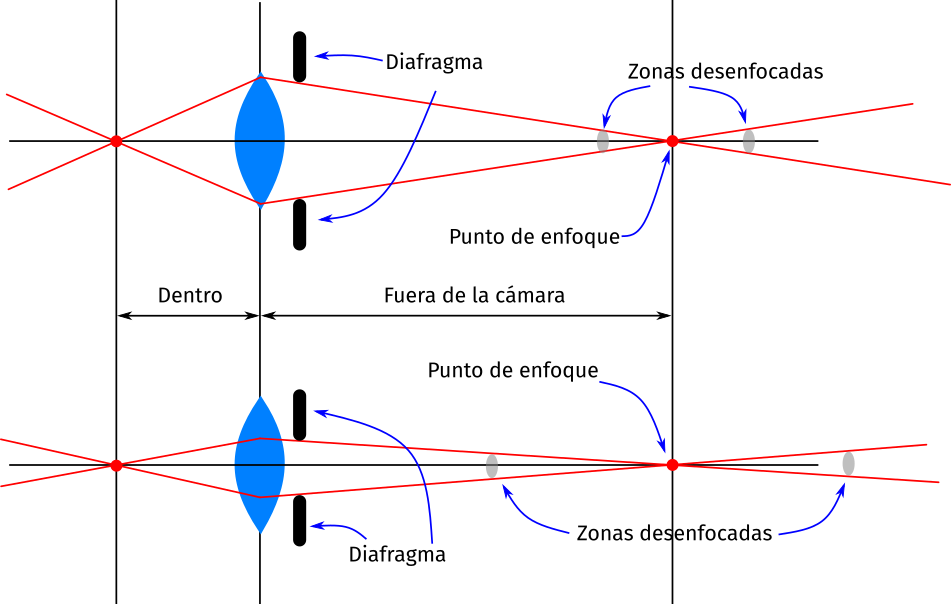
A simple vista podemos observar que cuanto más grande sea la lente más grande será el ángulo en el que se enfocan los objetos. No podemos cambiar el tamaño de la lente, sin embargo, podemos modificar el ángulo en el que incide la luz en ella obturador, que no sólo modifica la cantidad de luz que entra en la cámara, sino que también afecta al enfoque. A quienes les gusta la fotografía saben que cuando juegan con la apertura del diafragma del objetivo, consiguen un rango de objetos enfocados más amplio cuando utilizan aperturas más pequeñas. Sin embargo, a aperturas grandes enseguida los objetos situados un poco antes o después, quedan desenfocados.
Enfocar la cámara
Como hemos visto antes, el cálculo del enfoque necesita también la distancia focal f y la apertura de la lente. El registro de la cámara se modifica añadiendo ambos valores:
-record(camara, { origen = {0,0,0} % Posición de la cámara , mira = {0,0,-1} % Punto al que mira , sup = {0,1,0} % Orientación del lado superior de la cámara , angulo = 80 % Ángulo del campo de visión , apertura = 2.0 % Diámetro de la lente , f = 1.0}). % Distancia focal
El código de la cámara queda de la siguiente manera:
start(#camara{origen=Origen,mira=MiraA,sup=VArriba,angulo=CV,apertura=Apertura,f=Dist_Focal}, #config{ratio=Ratio,ancho=Ix,muestras=Muestras,profun=Profun,tesela=Tesela,procesos=Procesos}=Config) -> io:format("Estableciendo datos de la imagen...~n"), Pid = rerl_imagen:start(Config), register(imagen, Pid), io:format("Estableciendo datos de la cámara...~n"), Theta = rerl:grados_a_radianes(CV), % Calcular el ángulo en radianes del campo de visión H = math:tan(Theta / 2), Viewport_Alto = 2.0 * H, % Calcular el factor de altura de la imagen Viewport_Ancho = Viewport_Alto * Ratio, W = rerl:vector_unidad(rerl:resta(Origen, MiraA)), U = rerl:vector_unidad(rerl:cruz(VArriba, W)), V = rerl:cruz(W, U), Iy = round(Ix / Ratio), Horizontal = rerl:mul(rerl:mul(U, Viewport_Ancho), Dist_Focal), Vertical = rerl:mul(rerl:mul(V, Viewport_Alto), Dist_Focal), %% Eii = Origen - Viewport_Ancho/2 - Viewport_Alto/2 - {0,0,Focal} Medio_H = rerl:dividir(Horizontal, 2), Medio_V = rerl:dividir(Vertical, 2), Eii = rerl:resta( rerl:resta( rerl:resta(Origen, Medio_H), Medio_V), rerl:mul(W, Dist_Focal)), Estado = #state{origen=Origen , alto=Viewport_Alto , ancho=Viewport_Ancho , ix=Ix , iy=Iy , ratio=Ratio , u=U , v=V , horizontal=Horizontal , vertical=Vertical , eii=Eii , radio_lente = Apertura / 2 , muestras=Muestras , profundidad=Profun , tesela=Tesela , procesos=Procesos}, spawn(rerl_camara, init, [Estado]).
El cambio fundamental para conseguir el desenfoque o blur de las imágenes se da a la hora de lanzar los rayos:
%% %% Calcula la dirección de un nuevo rayo. El origen siempre es el %% origen de la cámara. %% lanza_rayo(#state{profundidad=Prf}=Estado, Cam, S, T) -> {Origen,Eii,U,V,R_Lente,Horizontal,Vertical} = Cam, {X,Y,_} = rerl:mul(rerl:random_en_disco_unidad(),R_Lente), %% Offset = U*X + V*Y, Offset = rerl:suma(rerl:mul(U, X), rerl:mul(V, Y)), %% Eii + Hor*U + Ver*V - Origen Dir = rerl:resta( rerl:resta( rerl:suma( rerl:suma( Eii, rerl:mul(Horizontal, S)), rerl:mul(Vertical, T)), Origen), Offset), O = rerl:suma(Origen, Offset), Rayo = #rayo{origen=O,dir=Dir}, color_rayo(Estado, Rayo, Prf).
El truco está en que en lugar de enviarlos desde el punto exacto del origen de la cámara, se utiliza un punto ligeramente distante de él según la distancia y la apertura. Para ello, hacemos que en lugar de un punto, sea un círculo.
Para ello necesitamos también una función que nos dé un punto aleatorio dentro de un disco de tamaño 1:
random_en_disco_unidad() -> P = {random(-1.0,1.0),random(-1.0,1.0),0}, M = modulo_cuadrado(P), if M >= 1 -> random_en_disco_unidad(); true -> P end.
Y tenemos nuestra imagen con desenfoque. Con una distancia focal de
1:1 obtenemos:

Cambiando la apertura a 1:25 obtenemos.

Supongo que está claro, no sólo por las explicaciones anteriores, sino también atendiendo a las imágenes obtenidas, que una apertura más pequeña (\(1/25\)) genera imágenes más enfocadas que una apertura más grande (\(1/1\)).
Conclusiones
Con esto hemos llegado al final del primer libro-tutorial de cómo
programar un raytracer. Tenemos una cámara plenamente funcional y
los materiales básicos: reflexión, refracción y color sólido.
Únicamente conoce una geometría: la esfera. Pero en definitiva es todo
lo que se espera de un raytracer. No lo he hecho en un fin de semana
porque era un plazo irreal y porque he perdido mucho tiempo en tareas
paralelas, como contarlo en el blog o traducir el código y el método
a erlang.
Por otro lado, el raytracer funciona de forma paralela, se pueden ajustar el número de procesos que lanzará y repartiendo la imagen en pequeñas partes, ─o grandes, porque también se puede configurar el tamaño─, al hacerlo.
A partir de aquí, me tengo que pensar si sigo con la serie de artículos, aunque quiero terminar la serie de los tres libros lo mismo es muy aburrido el monotema en el que casi se está convirtiendo el blog.
Footnotes:
Recordad que el objeto lo habíamos definido como un record
compuesto de geometría y material. Así pues, encontraremos las
definiciones de las geometrías y materiales en el fichero de la
escena.
Algunos programas dan soporte a 0-65535 colores por canal RBG, pero no todos.
Los aficionados a la fotografía (digital) estarán encantados con el artículo de hoy, ─espero─: formato raw, distancia focal, apertura de obturardos... hoy traigo de todo eso.
Por eso se ha elegido el ángulo de 80º como el valor por defecto para el campo de visión vertical al definir la cámara.


Comentarios