Hasta ahora todos los materiales tenían apenas un color y un índice de dispersión, porque todos eran del mismo tipo. Pero ahora, necesitaremos obtener qué tipo de material tiene el objeto. Es decir, ahora, los materiales son siempre difusos y el cálculo del material siempre es el mismo.

-record(material, { tipo       = nil           % Tipo de material
                  , albedo     = {0,0,0}       % Factor de atenuación de color
                  , dispersion = #rayo{}}).    % Factor de dispersión de la luz

Hasta este momento, el cálculo de la dispersión del material en un punto se venía efectuando dentro del mismo proceso de cálculo del pixel. Sin embargo, debido a la complejidad que encontraremos más adelante impone la necesidad de tener más código en un nuevo módulo que llamaremos rerl_material. Este fichero lo iniciamos con los cálculos de dispersión para el material difuso que es el único que veníamos utilizando hasta ahora.

-module(rerl_material).

-include("registros.hrl").

-export([dispersion_luz/1]).

%%%-------------------------------------------------------------------------
%%% cálculos del color para un impacto
%%%-------------------------------------------------------------------------

%%
%% Calcula la dispersión de la luz en basea M (material) e I (el impacto)
%%
dispersion_luz(#impacto{material=M}=I) ->
    case M of
        #material{tipo=difuso} ->
            Direccion_Dispersion =
                rerl:suma(rerl:suma(I#impacto.normal, I#impacto.p), rerl:random_vector_unidad()),
            Dispersion = #rayo{origen=I#impacto.p,dir=Direccion_Dispersion},
            M#material{dispersion=Dispersion};
        _ ->
            M#material{albedo={1.0,0.0,1.0}}
    end.

De esta manera, debemos modificar también el registro de material en el fichero mundo.rerl. Observese, que la dispersión se establece a nil y el material a difuso:

{objeto,{esfera,{0,0,-1},0.5},{material,difuso,{1.0,0.5,0.3},nil}}.
{objeto,{esfera,{0,-100.5,-1},100},{material,difuso,{0.5,0.3,1.0},nil}}.

El resultado es el siguiente:

Como podemos observar hemos conseguido nuestras dos esferas con un poco de color. Nada espectacular pero ya empieza a parecer un raytracer de verdad.

En el libro-tutorial que estoy siguiendo para programar este raytracer con erlang llaman a los materiales reflexivos metálicos. Por esto, yo he preferido llamarlo reflexion, no sólo los metales reflejan la luz, otros materiales también lo hacen. Reflejar el entorno lo hace cualquier superficie pulida, sea plástico, vidrio, líquido, etc.

En el libro, cómo calcular la reflexión comienza con una aproximación tal como se explica en la siguiente figura:

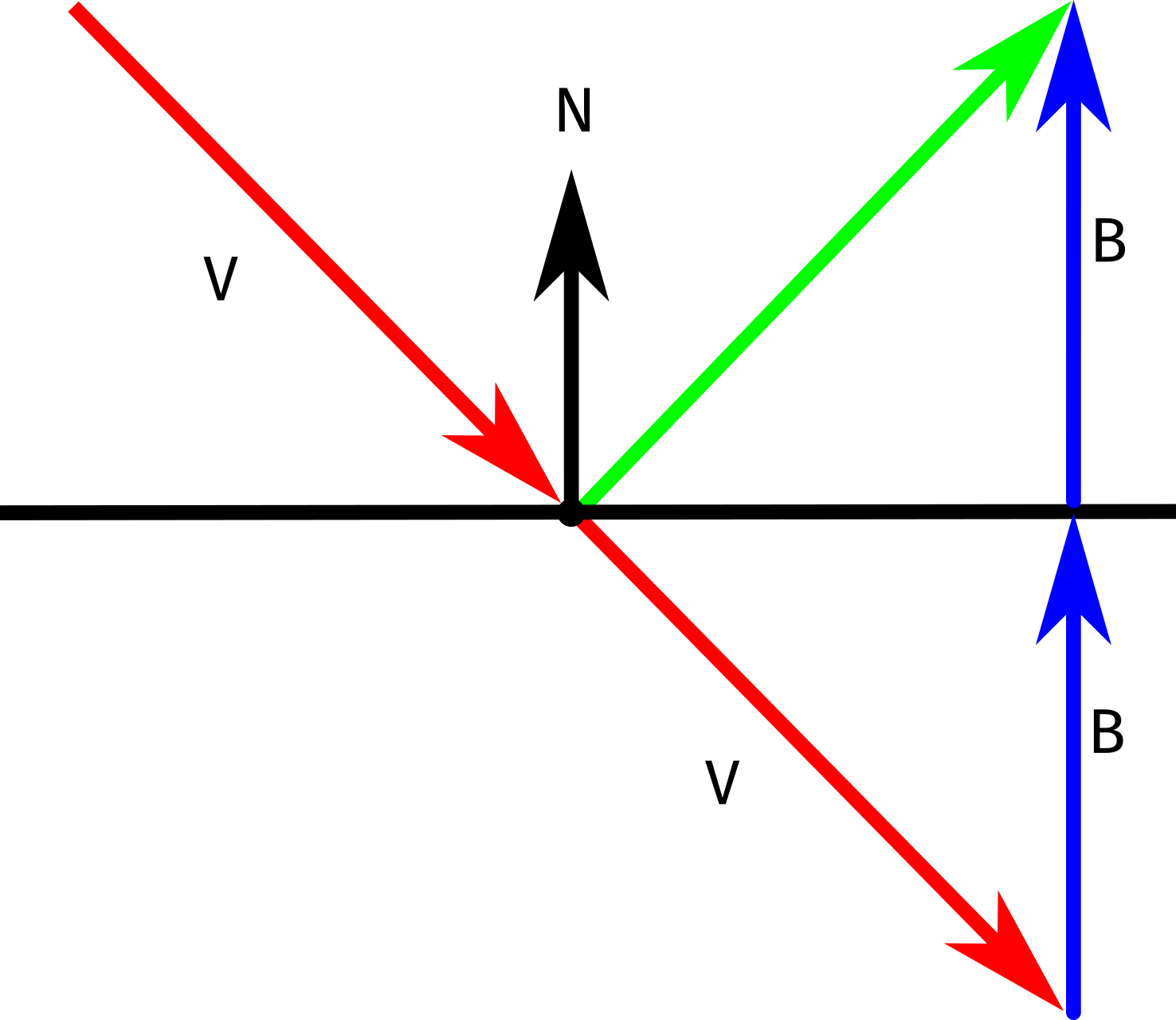
Como se ve, lo que se hace es continuar el rayo a partir del punto de impacto y luego calcular otro que vaya del punto de impacto a dos veces la distancia a la base del origen de la normal en el punto de impacto. Es decir, nuestros cálculos tienen que encontrar un vector con el mismo módulo que \(V\). Según la figura podemos decir que el rayo verde, el que estamos buscando es \(V + 2b\). Para calcular el largo de \(b\) podemos obtenerlo mediante \(V \cdot N\), puesto que, aunque nuestra normal \(N\) tiene una longitud de \(1\), puede ser que \(V\) no. Además, como los puntos que se encuentren dentro tienen valor negativo, la fórmula de la reflexión quedaría como:

\[R = V - 2 \times (V \cdot N) \times N\]

Traducida a nuestro código en el fichero rerl.erl aparece la siguiente función:

%%
%% Cálculo del vector (V) reflejado al incidir en una superficie con
%% normal (N).
%%
reflexion(V, N) ->
    resta(V, mul(N, 2 * punto(V, N))).

Luego, en la resolución del material llamaremos a esta función con el valor de la dirección del rayo que incide y la normal en ese punto.

La alternativa a estos cálculos hubiera sido calcular el ángulo de incidencia y reflejar el rayo con el ángulo equivalente, que son más costosos de calcular... y que ya los veremos en los cálculos de otros materiales que también reflejan.

Al añadir un nuevo material, nuestro fichero de materiales añaden también el cálculo de la dispersión para el tipo reflexion:

%%
%% Calcula la dispersión de la luz en basea M (material), I (el impacto) y
%% R (el rayo que incide).
%%
dispersion_luz(R, #impacto{material=M}=I) ->
    case M of
        #material{tipo=difuso} ->
            Direccion_Dispersion =
                rerl:suma(rerl:suma(I#impacto.normal, I#impacto.p), rerl:random_vector_unidad()),
            Dispersion = #rayo{origen=I#impacto.p,dir=Direccion_Dispersion},
            M#material{dispersion=Dispersion};
        #material{tipo=reflexion} ->
            Reflexion = rerl:reflexion(rerl:vector_unidad(R#rayo.dir), I#impacto.normal),
            Dispersion = #rayo{origen=I#impacto.p,dir=Reflexion},
            M#material{dispersion=Dispersion};
        _ ->
            M#material{albedo={1.0,0.0,1.0}}
    end.

Para probarlo, he modificado también el archivo mundo.rerl dejándolo así:

{objeto,{esfera,{0,0,-1},0.5},{material,difuso,{0.7,0.3,0.3},nil}}.
{objeto,{esfera,{0,-100.5,-1},100},{material,difuso,{0.8,0.8,0.0},nil}}.

{objeto,{esfera,{-1.0,0.0,-1.0},0.5},{material,reflexion,{0.8,0.8,0.8},nil}}.
{objeto,{esfera,{1.0,0.0,-1.0},0.5},{material,reflexion,{0.8,0.6,0.2},nil}}.

el resultado, al generar la imagen es:

Como se puede apreciar, la reflexión de la luz produce objetos de aspecto pulido y metálico. Pero no todos los metales están pulidos, así que vamos a por el siguiente paso.

En el libro los llaman materiales dieléctricos. No sé si será un falso amigo¹, pero en castellano el término dieléctrico se emplea para denominar a los materiales aislantes o que no conducen bien la electricidad. Sin embargo, en el libro lo utilizan para referirse a materiales transparentes... y no me parece que el agua sea mala conductora de la electricidad, precisamente.

La refracción se basa en la Ley de Snell o Descartes.

Básicamente, dicha ley establece que:

\[n_1 \cdot sen \theta_1 = n_2 \cdot sen \theta_2\]

donde \(n_1\) y \(n_2\) son los índices de refracción de dos medios en contacto. Cuando un rayo incide en una superficie con un ángulo \(\theta_1\) se transmite al siguiente medio con un ángulo \(\theta_2\).

Para calcular el ángulo con el que se refracta el rayo en el segundo medio, podemos despejar en la ecuación anterior:

\[sen \theta_2 = \frac{n_1}{n_2} \cdot sen \theta_1\]

En el lado de la refracción el rayo refractado \(R\), forma un ángulo \(\theta_2\) con la normal en ese lado. Pero podemos descomponer dicho rayo \(R\) en dos componentes: uno perpendicular a dicha normal y otro paralelo a la normal:

\[R = R_{perpend.} + R_{paralelo}\]

Si resolvemos estos componentes por separado tenemos:

\[R_{perpend.} = \frac{n_1}{n_2} (R_1 + cos \theta_1)\]

\[R_{paralelo} = - \sqrt{1 - |R_{perpend.}|^2} \cdot n_1\]

También tendremos que resolver \(cos \theta_1\), pero sabemos que el producto escalar de dos vectores lo podemos expresar como el producto de sus módulos con el coseno del ángulo que forman, es decir:

\[a \cdot b = |a| |b| cos \theta\]

Si lo restringimos el módulo de esos vectores a \(1\):

\[a \cdot b = cos \theta\]

Y por tanto, en las ecuaciones anteriores podemos escribir \(R_{perpend.}\) como

\[R_{perpend.} = \frac{n_1}{n_2} (R_1 + (-R_1 \cdot n_1)n_1)\]

Después de esta introducción matemática, el código para calcular la refracción en el fichero rerl.erl la dejamos de la siguiente manera:

%%
%% Cálculo del vector refractado al inicidir un rayo con dirección UV
%% en una superficie con normal N y un factor de refracción
%% determinado por N_div_N
%%
refraccion(UV, N, N_div_N) ->
    Coseno = punto(mul(UV, -1), N),
    R_perp = mul(suma(UV, mul(N, Coseno)), N_div_N),
    Raiz = math:sqrt(abs(1 - modulo_cuadrado(R_perp))),
    R_parl = mul(N, -Raiz),
    suma(R_perp, R_parl).

En los cálculos de la refracción, he preferido hacer algunos cálculos por partes para no perderme yo mismo. Sin embargo, se puede comprobar fácilmente que el código se corresponde con la fórmulas explicadas anteriormente.

Luego, en la parte de tratamiento de los materiales se ha añadido un apartado para los materiales transparentes:

dispersion_luz(R, #impacto{material=M,cara_frontal=Frontal}=I) ->
  case M of
      %% ....
      #material{tipo=transparente,ir=Ir} ->
          Ratio_Refraccion =
              case Frontal of
                  true ->
                      1.0 / Ir;
                  false ->
                      Ir
              end,
          Direccion_Unidad = rerl:vector_unidad(R#rayo.dir),      % Convertir la dirección en un vector módulo 1
          Refractado = rerl:refraccion(Direccion_Unidad, I#impacto.normal, Ratio_Refraccion),
          Dispersion = #rayo{origen=I#impacto.p,dir=Refractado},
          M#material{dispersion=Dispersion};
    _ ->
          ok
  end.

En la primera parte del código para este material comprobamos si el impacto es en la superficie exterior o la interior. Si el caso es que el choque es en la parte interna de la superficie tenemos que devolver el rayo a la trayectoria que traía en el aire. Después, simplemente se llama a la función explicada anteriormente para calcular la dispersión.

Convertí una de las esferas en transparente para ver cómo se veía y el código del mundo quedó así:

{objeto,{esfera,{0,0,-1},0.5},{material,difuso,{0.7,0.3,0.3},nil,nil,nil}}.
{objeto,{esfera,{0,-100.5,-1},100},{material,difuso,{0.2,0.2,0.0},nil,nil,nil}}.

{objeto,{esfera,{-1.0,0.0,-1.0},0.5},{material,transparente,{1.0,1.0,1.0},nil,1.5,nil}}.
{objeto,{esfera,{1.0,0.0,-1.0},0.5},{material,reflexion,{0.8,0.6,0.2},0.8,nil,nil}}.

El resultado obtenido es el siguiente:

Viendo ese resultado resulta que bueno, sí, es transparente y refracta la luz, pero ¿no es demasiado? ¿no resulta irreal? Sí, ¿no?

Eso es por una razón muy sencilla: no todos los rayos que impactan con una superficie transparente se refractan.

Cuando los rayos inciden en la superficie con un determinado ángulo se refracta, pero si ese ángulo es el ángulo crítico puede no conseguir refractarse y si sobrepasa dicho ángulo se refleja reflejarse.

Bueno, pues tenemos que volver a la Ley de Snell:

\[n_1 \cdot sen \theta_1 = n_2 \cdot sen \theta_2\]

Pero si consideramos que la esfera es de vidrio (índice de refracción \(n_1 = 1.5\)) y el entorno es aire (índice de refracción \(n_2 = 1.0\)), entonces:

\[sen \theta_2 = \frac{n_1}{n_2} \cdot sen \theta_1\]

Puesto que \(sen \theta_2\) no puede ser superior a \(1\)² si resulta que

\[sen \theta_2 = frac{n_1}{n_2} > 1.0\]

el rayo estará incidiendo en un ángulo en el que no puede refractarse y por tanto debería reflejarse. Algo que tenemos fácilmente podemos comprobar mirando el agua y viendo cómo se reflejan los objetos de la otra orilla del río y sin embargo vemos el fondo en la orilla a nuestros pies. A eso se le llama reflectancia o refelctividad.

Bien, vale, pero ¿cómo calculamos el \(sen \theta\)? Pues vamos a partir de la ecuación básica de la trigonometría:

\[1 = sen^2 \theta + cos^2 \theta\]

y si despejamos

\[sen \theta = \sqrt{1 - cos^2 \theta}\]

y como vimos antes

\[cos \theta = R \cdot n\]

donde \(R\) es la dirección del rayo que incide y \(n\) la normal del punto, si su módulo es igual a 1, como hicimos antes. Puedo enrollarme con más explicaciones, pero creo que está suficientemente claro el proceso de razonamiento.

El código que resume todas estas disquisiciones queda así:

#material{tipo=transparente,ir=Ir} ->
    Ratio_Refraccion =
        case Frontal of
            true ->
                1.0 / Ir;
            false ->
                Ir
        end,
    Direccion_Unidad = rerl:vector_unidad(R#rayo.dir),
    Coseno = min(rerl:punto(rerl:mul(Direccion_Unidad, -1), I#impacto.normal), 1.0),
    Seno = math:sqrt(1 - Coseno * Coseno),
    No_Refracta = Seno * Ratio_Refraccion > 1,
    Refractado =
        case No_Refracta of
            true ->
                %% Si no refracta, refleja
                rerl:reflexion(Direccion_Unidad, I#impacto.normal);
            false ->
                rerl:refraccion(Direccion_Unidad, I#impacto.normal, Ratio_Refraccion)
        end,
    Dispersion = #rayo{origen=I#impacto.p,dir=Refractado},
    M#material{dispersion=Dispersion};

Es decir, se comprueba si el rayo refleja o refracta y se utiliza una fórmula u otra según el caso.

Para el mismo mundo el resultado es:

Puede parecer que a simple vista no hay mucha diferencia con el método anterior pero no es así. Lo que ocurre es que parece que sólo se aplica la reflexión a los rayos que han conseguido entrar en el objeto... faltan los rayos reflejados en el exterior. También se puede apreciar en el tiempo de render, puesto que las reflexiones cuesta menos calcularlas que las refracciones.

Aún nos queda calcular la reflectancia o refelctividad exterior para tener un material más ajustado a la realidad. Pero ésta tiene una fórmula compleja. En el libro-tutorial que estoy siguiendo utiliza la aproximación polinomial de Christopher Schlick afirmando que es suficientemente precisa. La fórmula sería:

\[Reflectancia = r_0 + (1 - r_0) \times (1 - cos \theta)^5\]

donde \(r_0 = (\frac{1-i_r}{1+i_r})^2\) siendo \(i_r\) el índice de refracción.

Traduciéndolo a código en el fichero rerl.erl nos queda dicha aproximación así:

%%
%% Calcula la reflectancia de una superficie en base al coseno (Cos)
%% del ángulo con que se mira y el índice de refracción Ir.
reflectancia(Cos, Ir) ->
    R = (1 - Ir) / (1 + Ir),
    R0 = R * R,
    R0 + (1 - R0) * math:pow((1 - Cos), 5).

Además, para tenerla en cuenta en nuestro material, el código es el siguiente:

#material{tipo=transparente,ir=Ir} ->
    Ratio_Refraccion =
        case Frontal of
            true ->
                1.0 / Ir;
            false ->
                Ir
        end,
    Direccion_Unidad = rerl:vector_unidad(R#rayo.dir),
    Coseno = min(rerl:punto(rerl:mul(Direccion_Unidad, -1), I#impacto.normal), 1.0),
    Seno = math:sqrt(1 - Coseno * Coseno),
    No_Refracta = (Seno * Ratio_Refraccion > 1) orelse (rerl:reflectancia(Coseno, Ratio_Refraccion) > rerl:random()),
    Refractado =
        case No_Refracta of
            true ->
                %% Si no refracta, refleja
                rerl:reflexion(Direccion_Unidad, I#impacto.normal);
            false ->
                rerl:refraccion(Direccion_Unidad, I#impacto.normal, Ratio_Refraccion)
        end,
    Dispersion = #rayo{origen=I#impacto.p,dir=Refractado},
    M#material{dispersion=Dispersion};

Como se puede apreciar, se añadido otra condición para no refractar y reflejarse, el resto del código se mantiene exactamente igual.

Para mostrar mejor el efecto de la reflectancia he cambiado algunos parámetros de la imagen: la he hecho de 800 de ancho y he subido las muestras a 500 en lugar de las 100 habituales. El resultado conseguido es éste:

Se puede apreciar el reflejo de la bola central en nuestra bola transparente (aunque se aprecia mejor en las zonas oscuras). También podemos ver el reflejo del fondo sobre la parte superior de la bola transparente. En esa imagen tenemos ejemplos de los tres materiales básicos. Nuestro raytracer va tomando forma.

Por último, en la versión actual se ha remodelado el proceso de render. Hasta ahora venía haciéndose desde el fichero rerl.erl, cuya función principal es contener las funciones de cálculo comunes a todos los demás procesos.

Se ha creado un fichero escena.erl cuya única función es generar el proceso de imagen, crear los objetos que intervienen en la escena, crear la cámara, ajustarla y ponerla en marcha. El código ha quedado así:

-module(escena).

-include("registros.hrl").

-export([escena/0]).

escena() ->
    Nombre = "imagen.ppm",                  % Nombre del fichero de imagen generado
    O = {0,0,0},                            % Origen de la cámara
    Ratio = 16 / 9,                         % Ratio ancho/alto de la imagen
    Ancho = 400,                            % Ancho en puntos de la imagen
    Muestras = 100,                         % Nº de muestras por pixel
    Profun = 50,                            % Número de «rebotes» por rayo.
    Tesela = 25,                            % Tamaño del lado de la tesela en puntos
    Procesos = 10,                          % Número de procesos de cálculo

    %% Preparar la imagen para el render
    Pid = rerl_imagen:start({Ancho,Ratio,Nombre}),
    register(imagen, Pid),

    %% Materiales
    Material_Suelo = #material{tipo=difuso,albedo={0.2,0.2,0.0}},
    Difuso = #material{tipo=difuso,albedo={0.7,0.3,0.3}},
    Cristal = #material{tipo=transparente,albedo={1.0,1.0,1.0},ir=1.5},
    Metal = #material{tipo=reflexion,albedo={0.8,0.6,0.2},rugoso=0.3},

    %% Esferas
    Esfera_Suelo = #esfera{centro={0,-100.5,-1},radio=100},
    Esfera_Central = #esfera{centro={0,0,-1},radio=0.5},
    Esfera_Izda = #esfera{centro={-1.0,0.0,-1.0},radio=0.5},
    Esfera_Dcha = #esfera{centro={1.0,0.0,-1.0},radio=0.5},

    %% Montar los objetos
    Objs = [#objeto{geom=Esfera_Central,material=Difuso}
          , #objeto{geom=Esfera_Suelo,material=Material_Suelo}
          , #objeto{geom=Esfera_Izda,material=Cristal}
          , #objeto{geom=Esfera_Dcha,material=Metal}],

    io:format("Iniciando la cámara...~n"),
    Pid_camara = rerl_camara:start({O,Ratio,Ancho,Muestras,Profun}),
    register(camara, Pid_camara),

    %% Preparar procesos y lanzar el render
    camara ! {mosaico,Tesela,Procesos},
    camara ! {render,Objs}.

El proceso es casi el mismo. Sin embargo, hay que remarcar que después de establecer los datos del render y la imagen se crean los materiales y objetos que van a formar parte del mundo que hay generar. Por tanto, prescindimos del archivo mundo.rerl que veníamos utilizando hasta ahora, ─como hemos visto en los apartados anteriores─. A partir de ahora, las modificaciones en la escena se harán en este fichero.

Además, las funciones de reflexión y refracción de la luz se han movido al módulo rerl_material, puesto que únicamente se llaman desde él.

Alguien³ me preguntó por el tipo de iluminación que se emplea en el libro. La respuesta corta es Ambient Occlusion. Es un sistema de iluminación quizá más complejo de explicar que otros que necesitan fuentes de luz. La base de este tipo de iluminación consiste en calcular la luz ambiente, la que rebota de objetos a objetos.

Suele calcularse como:

\[A_{(\omega,n)} = \frac{1}{\pi} \int_{\omega \in \Omega} V_{(x,\omega)} |\omega \cdot n| d\omega\]

Al no haber fuentes de luz, la iluminación se parece a un día nublado, sin sombras contrastadas. En nuestro caso, la intensidad de la luz dependerá también del color del fondo. Cuanto más claro es el fondo más iluminación hay.

Por ejemplo, si elegimos colores más oscuros para nuestro fondo:

rerl:suma(rerl:mul({0.2,0.0,0.2}, (1-T)),
          rerl:mul({0.1,0.3,0.5},  T))

obtenemos:

Esta segunda imagen está generada con un fondo absolutamente blanco, para que se pueda comparar la diferencia en la iluminación de ambas imágenes.

No podría decir por qué el autor del tutorial ha elegido esa iluminación para la parte más básica del raytracer. Supongo, y es una impresión totalmente subjetiva mía, que aunque es más difícil de explicar, ─de hecho no lo explica en ningún sitio del libro y además su computación es más exigente que para otros modelos de iluminación, como la tipo phong que necesita fuentes de luz─, le ha permitido generar imágenes desde el minuto cero del tutorial e ir añadiendo características sin crear ningún tipo de objeto luminoso. Pero ya digo, que es una especulación mía.

Nuestro raytracer va tomando forma poco a poco, aunque aún está en mantillas ya que sólo admite como geometría de los objetos la esfera, los materiales hacen su función de una manera solvente. Además, cuenta con un procesamiento en paralelo de la imagen.

En las siguientes entregas nos meteremos más a fondo con la cámara haciendo que pueda variar su posición, su orientación, dotarla de zoom y profundidad de campo... en fin, hacerla parecer más una cámara completa.