Material difuso y corrección gamma
Pues aquí estoy de nuevo con otra entrega del raytracer y todo lo
que voy haciendo. Hoy voy a comenzar explicando cómo tengo configurado
Emacs para trabajar con erlang, porque me lo habéis pedido y luego
continuaré con las propuestas del libro... el de escribir un
raytracer en un fin de semana. Concretamente hablaré sobre el primer
material (el difuso) que propone y la corrección gamma del color.
Algunos me habéis preguntado cosas y otros me habéis mostrado un profundo aburrimiento con mi frikada. No puedo adelantar si esta serie durará mucho, ya siento aburriros, pero sois tan libres de no leerlo como yo de escribirlo. Por otro lado, hay quien quiere saber más, se queja de que voy lento y me pide que le dé más caña. Pero también hay quien ya se cansó en el primer artículo. Como he dicho antes, traigo otros pequeños avances: nuestras esferas representadas por primera vez con un material, ─en este caso, difuso─, y algunas cosillas más, como la corrección gamma del color y otros apuntes sobre las herramientas que estoy utilizando.
Voy a empezar por esta última, porque se debe a un pregunta que me han hecho: ¿Qué usas para hacerlo? La respuesta corta hubiera sido Emacs, pero conociendo al que me la ha hecho, estoy seguro de que se refiere a cosas más concretas.
Configuración de Emacs para programar en erlang
El hecho de programar con erlang, siendo un lenguaje minoritario, no
cuenta con la profusión de herramientas que otros lenguajes tienen
para la edición, depuración y mantenimiento del código. De hecho, la
mayoría de las aplicaciones que sirven para ello, vienen con el propio
erlang: observer, debugger, etc. que se pueden lanzar desde la
consola, o shell, de erlang con llamando a observer:start() o
debugger:start().
Si ya tienes instalado algún IDE como eclipse o IntelliJ, puedes
instalarte el plugin de erlang. No los he probado, pero
seguramente, conociendo ambos IDE's, serán unos paquetes que
funcionarán perfectamente y proporcionarán herramientas más allá del
coloreado de sintaxis.
A mí, esos IDE's me resultan demasiado pesados, complejos y prolijos,
llenos de botones situados por todas partes y, como sabéis, me decanto
más por un editor como Emacs. ¿Tengo que renunciar a muchas cosas
eligiendo un editor en lugar de un IDE? Pues no, prácticamente a
ninguna. Como digo, erlang trae sus propias aplicaciones de debug
y de visualizador de procesos1... y para lo demás está Emacs.
Paquetes para trabajar con erlang
Para trabajar con este lenguaje tengo tres paquetes instalados en Emacs que para mí son los básicos. En la lista de paquetes podréis encontrarlos, hay más2. Pero los que yo uso son éstos y me son suficientes:
erlang: el paquete general, con coloreado de sintaxis, indentación y algunas herramientas adicionales.company-erlang: para el autocompletado del código concompany.ivy-erlang-company: autocompletado company conivy-mode3.
El segundo y el tercero no merecen demasiada atención, si ya tienes
configurado ivy y company para otros lenguajes, por ello de ese
trío me voy a concentrar en el primero. El paquete erlang es muy
fácil de configurar y no necesitas más que añadir a tu init.el una o
dos líneas, o tres según las herramientas que uses. En mi caso:
(require 'erlang-start) (setq erlang-root-dir "/usr/lib64/erlang") (require 'erlang-flymake)
La primera línea inicia el paquete erlang en nuestro Emacs. La
segunda establece dónde está instalado. En OpenSuSe Tumbleweed se
instala en el path que veis arriba. Por defecto, el directorio
esperado es /usr/local/erlang. Si efectivamente lo tienes instalado
en ese directorio o creas un enlace para dicha dirección, no necesitas
ajustar la variable erlang-root-dir. En ese directorio, Emacs
buscará no sólo los ejecutables y librerías, sino también la
documentación. Y creedme, que es un lujo pulsar C-c C-d y que
Emacs te abra la documentación de la librería o de la función sobre
la que se encuentre el cursor para consultarla.
La tercera línea de la configuración activa flymake para erlang.
Si no utilizáis flymake tampoco la necesitas. Lo veremos enseguida,
pero primero vamos a ver qué combinaciones de teclas utilizo más
frecuentemente:
C-c C-c,comment-region: Comenta las lineas de código seleccionadas.C-c C-u,uncomment-region: Habilita el código comentado por el método anterior.C-c C-d,erlang-man-function-no-prompt: Muestra la página de manual deerlangde la función en la que se encuentra el cursor.C-c C-k,erlang-compile: compila el módulo que estamos editando.C-c C-q,erlang-indent-function: reorganiza el indentado de la función al estilo deerlang.C-c C-z,erlang-shell-display: abre un buffer con un shell deerlang.
Quizá lo más remarcable del paquete erlang son los skeletons. Los
skeletons son plantillas de código erlang. Hay desde módulos
completos para application, gen_server, supervisores, funciones
y estructuras de código más habituales como receive, cabeceras,
módulos, etc. Se pueden cargar desde el menú de Emacs o desde
comando con M-x tempo-template-erlang-* ... donde el * se
sustituye con el nombre del código que queramos, como small-header o
small-server, application, etc.
flymake
flymake es una herramienta que va compilando el código que estamos
escribiendo y notificando sus errores y avisos (warnings). No es
específica para erlang, de hecho encontraréis en la lista de
paquetes de ELPA todo un listado de ellas, porque cada lenguaje
tiene su correspondiente paquete. Sin embargo, no busquéis en esa
lista el paquete de erlang, no está.
En el caso de erlang el archivo erlang-flymake lo proporciona el
mismo paquete erlang. Por eso lo activamos en la configuración junto
a él.
El paquete flymake nos proporciona información muy valiosa para
encontrar errores de sintaxis avisándonos de varias maneras. En
formato texto podemos ver los siguientes avisos:
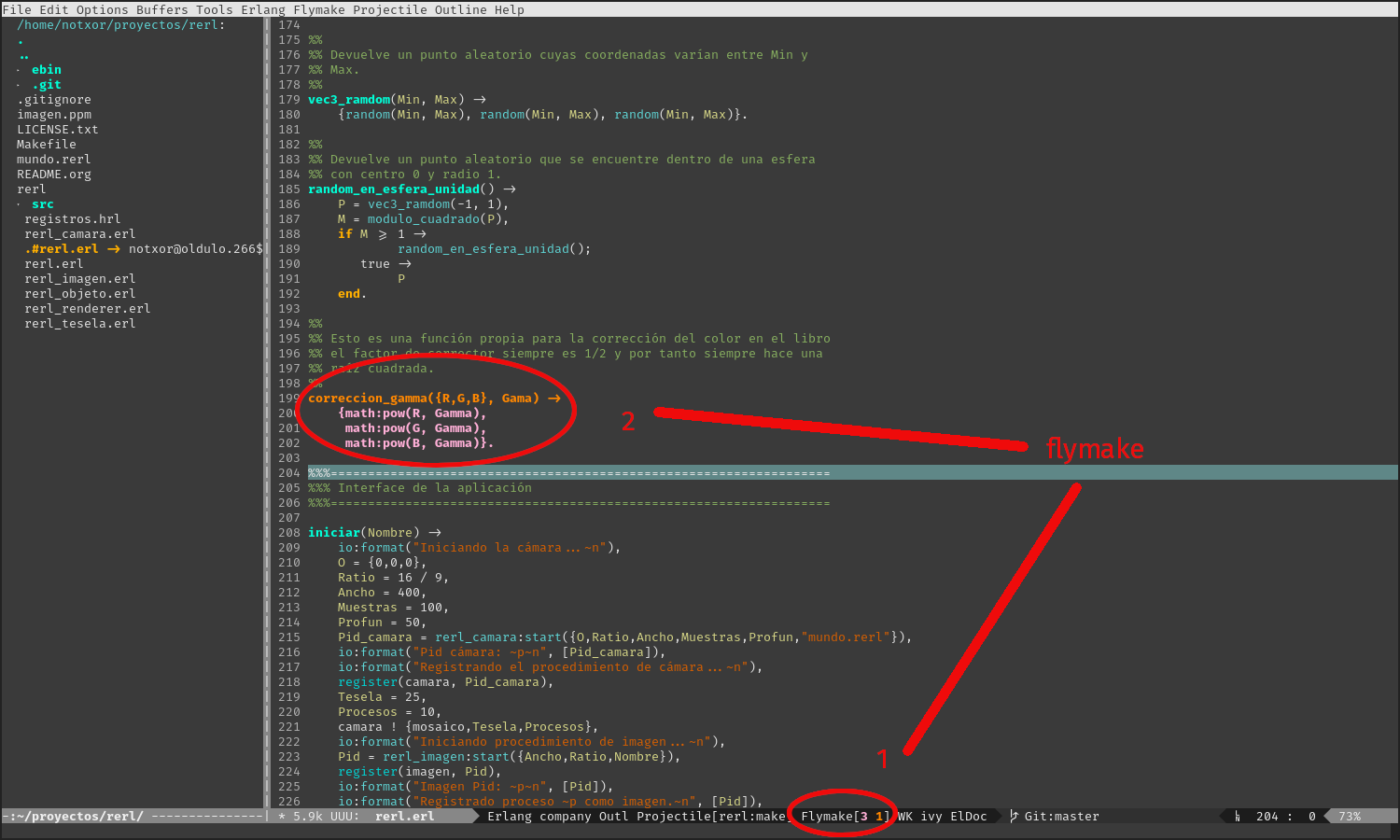
Como podemos ver en la imagen, en 1, vemos que en la línea de estado
de Emacs aparece [Flymake[3 1], es decir: hay 3 errores y 1
aviso. En \(2\) se encuentra una función donde están los errores. En la
imagen los errores se marcan en rosa y el aviso en naranja. Visto
así, no hay mucha información más que existen esos errores y
warnings. Si necesitamos más información, podemos apelar a M-x
flymake-show-diagnostics o M-x flymake-show-diagnostics-buffer.
Esta segunda hace que se muestre un buffer con esos errores tal y
como los da el compilador:
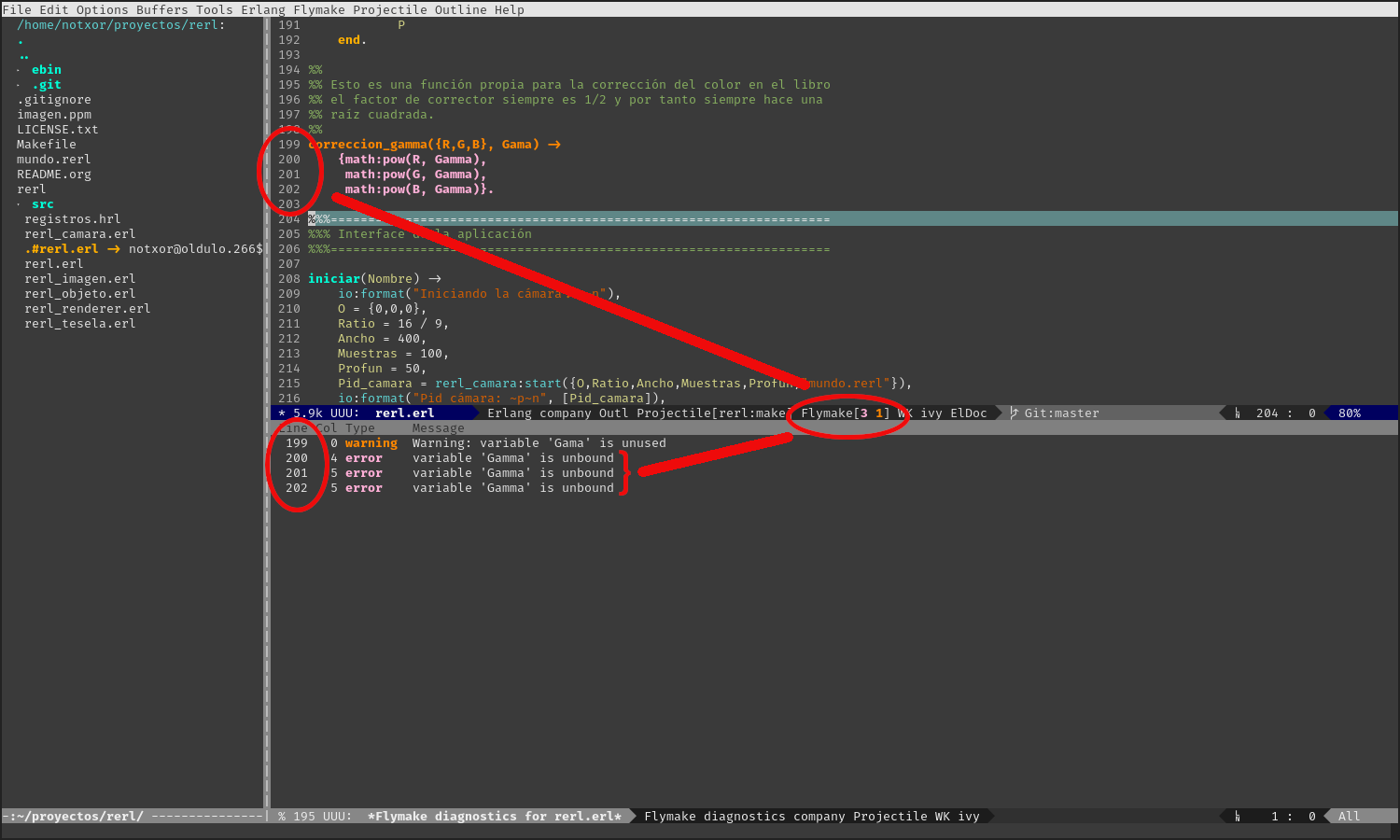
Como podemos ver, en el buffer un desglose con las líneas donde se han encontrado los errores y el tipo de error.
En modo gráfico la información es la misma pero presentada de manera más gráfica:
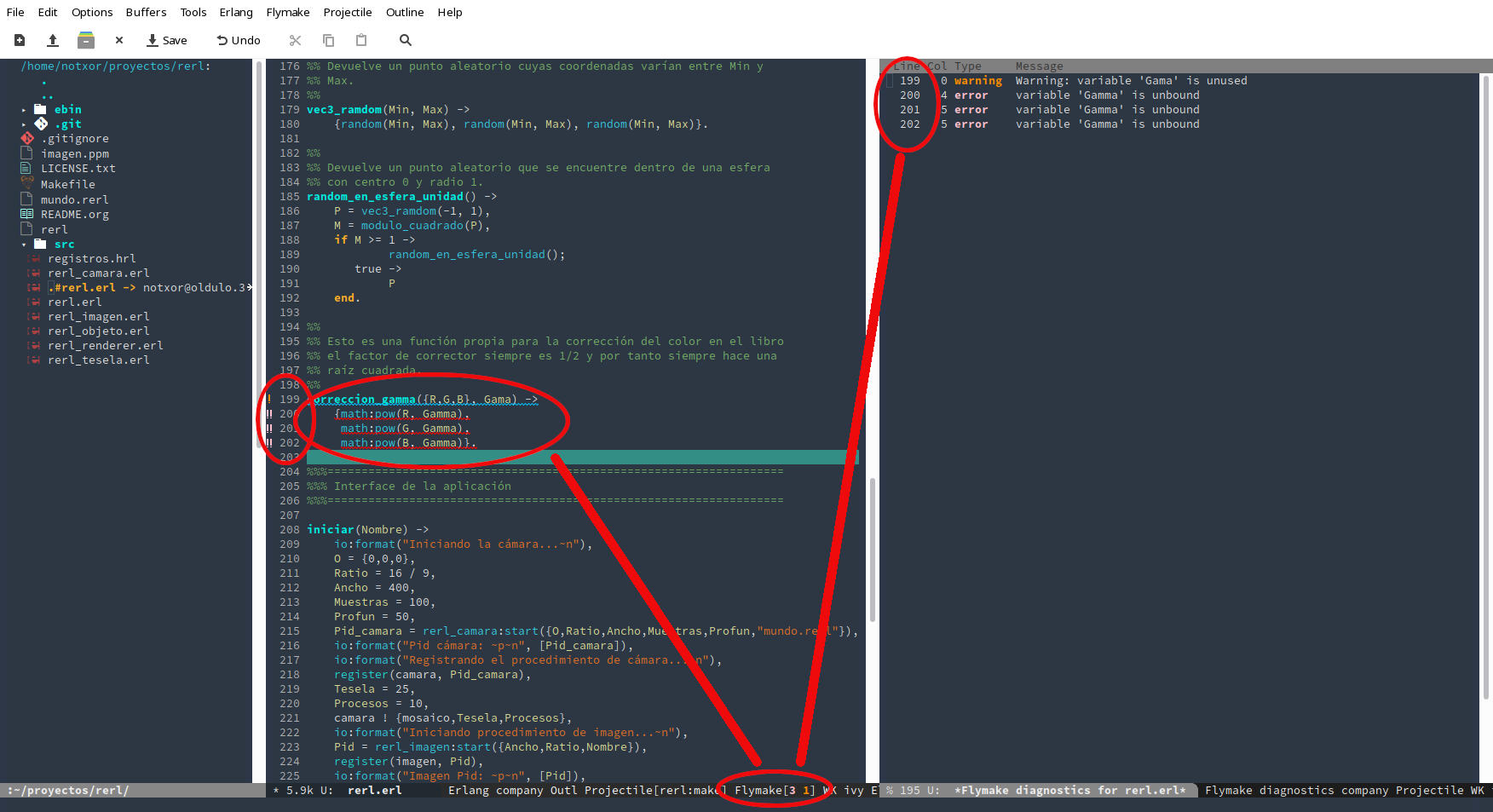
Como se puede ver, en el margen aparecen los símbolos ! para los
warnings y !! para los errores. Además subrayan los errores en
rojo y los warnings en azul. También se puede pinchar en la barra de
estado justo sobre Flymake y nos aparecerá un menú que nos permite
una serie de acciones, como por ejemplo, abrir el buffer de
diagnóstico... para aquellos que gustan de despegar su mano del
teclado para ir al ratón.
projectile y magit
Además lo que casi convierte Emacs en un IDE son las herramientas de
projectile y magit. En realidad, ambas, no tienen nada de
específico para trabajar con código erlang, pero sí son potentes
herramientas para trabajar con código en general.
La primera, projectile, proporciona herramientas y comandos para
trabajar sobre conjuntos de ficheros fuente agrupados en proyectos.
Tiene muchas funciones útiles para gestionarlos, pero lo que más estoy
utilizando es la opción de compilar el proyecto con C-c p c, o
buscar algo dentro del proyecto con C-c p s4.
La segunda, magit, es una de esas aplicaciones de Emacs que
aparece en todas partes como ejemplo de calidad. Sirve para gestionar
un proyecto con git y permite hacer de todo, aparte de lo habitual
de subir cambios, actualizar el repositorio o hacer commits: crear
ramas locales y remotas, rebase, merge o cualquier otro comando
que admita git, con especial mención a log o diff.
Si no has probado estas herramientas ya estás tardando en probarlas. Y como ya he hablado sobre ellas en otras ocasiones en el blog pues permitidme que lo deje aquí y dedique el artículo a los avances que he ido haciendo en el raytracer.
Primer material diffuse
El material difuso es un tipo de material que produce sólidos con aspecto mate. Si no entiendes exactamente a qué tipo de objetos me refiero, piensa en una goma de borrar o, en general, en cualquier tipo de goma. Este tipo de material presenta un aspecto rugoso o granulado, de forma que la luz al incidir sobre este tipo de superficies puede salir rebotada en cualquier dirección al azar y no reflejando el entorno:
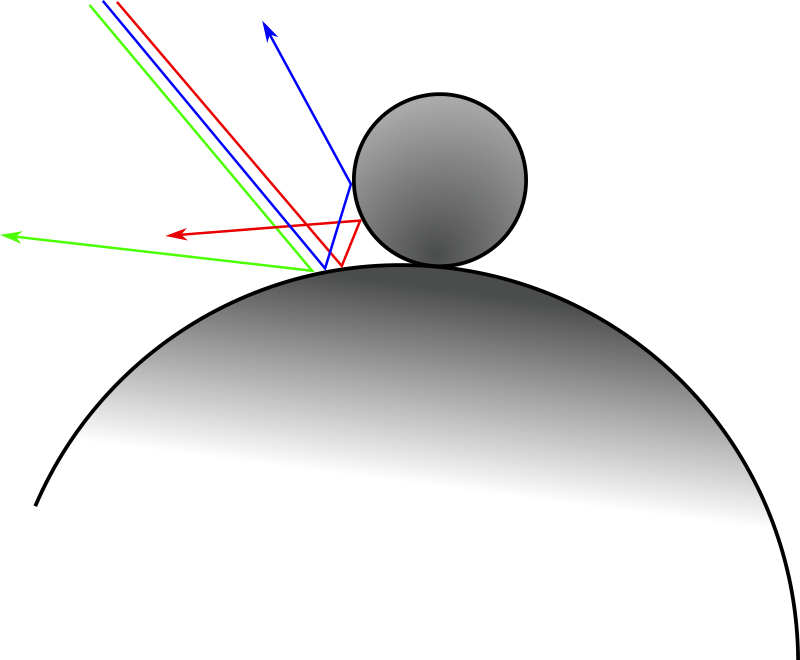
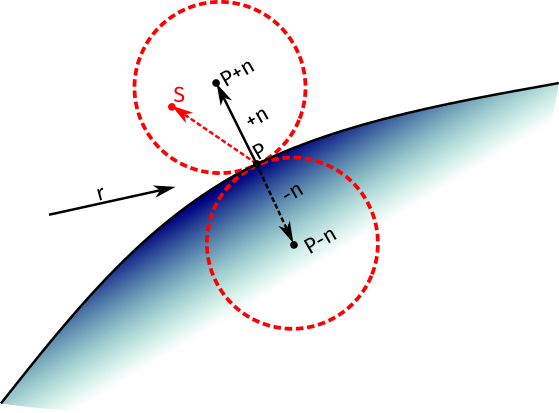
Siendo la superficie rugosa, los rayos de luz pueden rebotar en cualquier dirección. El algoritmo más utilizado para este tipo de materiales es el conocido como Lambert. Sin embargo, el libro comienza con una aproximación que se supone algo menos exigente con los cálculos. Esta aproximación propone crear dos esferas de puntos tal que, dado el punto \(P\) donde incide el rayo se considera el centro de una de ellas en \(P + \overrightarrow{n}\) y el centro de la otra en \(P - \overrightarrow{n}\). De estas dos, la primera se considera que está fuera de la superficie donde incide el rayo tangente a esa superficie en ese mismo punto, mientras que la segunda estaría dentro del objeto.
Básicamente, lo que hace es lanzar otro rayo cuando el rayo \(r\) incide en el punto \(P\). Entonces, al azar, se obtiene el punto \(S\) dentro de lo que sería la esfera de radio 1, para formar el vector \((S - P)\):
Esta aproximación se traduce en el código en la creación de unas
funciones muy sencillas, algunas como vec3_random/2 genera un punto
aleatorio que luego pediremos que esté entre -1 y 1.
%% %% Devuelve un punto aleatorio cuyas coordenadas están entre 0 y 1 %% vec3_ramdom() -> {random(),random(),random()}. %% %% Devuelve un punto aleatorio cuyas coordenadas varían entre Min y %% Max. %% vec3_ramdom(Min, Max) -> {random(Min, Max), random(Min, Max), random(Min, Max)}. %% %% Devuelve un punto aleatorio que se encuentre dentro de una esfera %% con centro 0 y radio 1. random_en_esfera_unidad() -> P = vec3_ramdom(-1, 1), M = modulo_cuadrado(P), if M >= 1 -> random_en_esfera_unidad(); true -> P end.
Hasta ahora la función color_rayo generaba el color basándose en la
normal del punto donde incidía el rayo y, por tanto, le bastaba con
conocer el rayo. Sin embargo, se ha modificado la función a color_rayo/3:
%% %% Calcula el color obtenido por un rayo particular %% color_rayo(_Estado, _Rayo, 0) -> {0.0,0.0,0.0}; color_rayo(Estado, Rayo, Contador) -> Impactos = impactos(Estado, Rayo, 0.001, ?INFINITO), Orden_impactos = lists:sort( fun(I,J) -> {_,#impacto{t=T1}} = I, {_,#impacto{t=T2}} = J, T1 < T2 end, Impactos), Impacto_Cercano = hd(Orden_impactos), case Impacto_Cercano of {true,Im} -> Objetivo = rerl:suma(rerl:suma(Im#impacto.normal,Im#impacto.p), rerl:random_en_esfera_unidad()), R = #rayo{origen=Im#impacto.p,dir=rerl:resta(Objetivo, Im#impacto.p)}, rerl:mul(color_rayo(Estado, R, Contador - 1), 0.5); % Ojo recursión {false,_} -> #rayo{dir=Dir} = Rayo, {_,Y,_} = rerl:vector_unidad(Dir), T = 0.5 * (Y + 1), rerl:suma(rerl:mul({1.0,1.0,1.0}, (1-T)), % Del color blanco {1,1,1} rerl:mul({0.5,0.7,1.0}, T)) % al color azul {0.5,07,1.0} end.
Se puede observar que se ha convertido en una función recursiva,
porque sigue el rayo donde impacta y puede seguirlo las veces que sea
necesario. Como podría darse el caso de que el rayo estuviera
rebotando infinitas veces, se pone una limitación con contador, que lo
hará sólo las veces que se determine por parámetro. Hacer notar
también que en la llamada a impactos/4 se ha establecido una
distancia Tmin de 0.001, hasta ahora se venía utilizando el valor
0, pero en los cálculos se consideraban valores como 0.0000001
como significativos y a estas alturas podemos considerar que es
suficiente con una milésima para la aproximación a 0.
Con todo esto el resultado obtenido es:

La imagen obtenida es suficientemente prometedora, aunque algo oscura. Nos podemos preguntar si hemos hecho algo mal para que nuestras esferas tengan un color gris tan oscuro. Sin embargo, la explicación viene de una característica de nuestro sistema visual: su adaptación a las diferentes intensidades de luz. Necesitamos ajustar los colores de la imagen a cómo lo verían nuestros ojos en una situación lumínica similar. Para ello se utiliza la corrección gamma del color.
El cálculo de la superficie utilizando el procedimiento de Lambert tampoco es muy compleja ni necesita mucho más tiempo. En mi máquina ha sido al revés, se ha calculado más rápido que la aproximación.

La distribución del color en la fórmula de Lambert se distribuye según el ángulo que forme la normal con el vector calculado, pudiendo llegar a \(cos^3 \phi\).
%% %% Devuelve un punto según la distribución de Lambert. %% random_vector_unidad() -> A = random(0.0, 2 * ?PI), Z = random(-1.0, 1.0), R = math:sqrt(1 - Z * Z), {R * math:cos(A), R * math:sin(A), Z}.
Sustituyendo la anterior llamada a random_en_esfera_unidad/0 por
random_vector_unidad/0 en el código del cálculo de color del pixel
se obtiene:

Si comparamos ambas imágenes calculadas, utilizando una aproximación la primera y utilizando la distribución de Lambert la segunda, son muy similares. Ésta última tiene unas sombras más suaves y quizá parezcan algo más luminosas ambas esferas.
Refactorización del código
Tras una pequeña refactorización del código, he metido todos los cálculos necesarios para realizar la imagen en los procesos tesela. Los objetos dejan de intervenir en los cálculos y se ha reducido el tiempo de render de la imagen anterior a unos 40 segundos. Una tercera parte, aproximadamente de lo que se empleaba antes. Más remarcable, si cabe porque no sólo calcula los mismos samples sino que además tiene que calcular los diferentes rayos para el material.
Corrección gamma
En el libro que estoy siguiendo para hacer este raytracer se limita a meter una corrección gamma calculando la raíz cuadrada del color que viene calculado. Sin embargo, he preferido cambiar la fórmula a una más general y acorde con las matemáticas:
\[V_f = A \cdot V_0^\gamma \]
que traducida a código se convierte en:
correccion_gamma({R,G,B}, Gamma) -> {math:pow(R, Gamma), math:pow(G, Gamma), math:pow(B, Gamma)}.
Como se puede observar la corrección \(\gamma\) es una potencia donde el valor final, \(V_f\), es el resultado de multiplicar el valor inicial, \(V_0\), por una constante \(A\) después elevarlo a \(\gamma\). Por tanto, si en el libro hacen una raíz cuadrada simplemente, están haciendo \(A=1\) y \(\gamma=1/2\).
La función de corrección la he puesto en el código que escribe el color del pixel en memoria:
{pixel_color,Pixel,Color} ->
#state{lienzo=Lienzo,pixeles=Px} = Estado,
Nuevo_lienzo = maps:put(Pixel, rerl:correccion_gamma(Color, 1/2), Lienzo),
Faltan = Px - 1,
Nuevo_Estado = Estado#state{lienzo=Nuevo_lienzo,pixeles=Faltan},
if Faltan < 1 ->
Tiempo = erlang:monotonic_time(millisecond) - Estado#state.tiempo,
io:format("~nTiempo empleado en segundos: ~p~n", [Tiempo / 1000]),
io:format("Escribiendo imagen...~n"),
escribir_imagen(Nuevo_Estado);
true ->
ok
end,
loop(Nuevo_Estado);
Explicar con detalle cómo funciona la corrección gamma sería muy largo, pero si vemos la serie de imágenes




podemos percatarnos que valores superiores a \(1\) harán las imágenes más oscuras mientras que valores inferiores a \(1\) harán las imágenes más luminosas.
Footnotes:
De procesos, de aplicaciones, de tablas de las bases de datos,
de consumo de memoria y procesador... en fin, todo lo que esté
moviendo el nodo erlang que se quiera analizar.
edts es otro paquete, no lo he probado, pero parece basarse
en otros paquetes, como los anteriores para hacer su trabajo.
Éste se instaló como dependencia, así que no me preocupo por él.
Da la opción de buscar con distintas herramientas como grep o
ag, que deben estar instaladas en el sistema, junto con su
correspondiente paquete de Emacs. grep suele estar instalado por
defecto, pero no así ag.


Comentarios