Ya lo expliqué, aunque en un solo párrafo y de forma rápida, más bien atropellada, porque pensé que a estas alturas el que más y el que menos ya lo sabría. Pero me habéis hecho preguntas que me hacen sospechar que no tenéis claro cómo funciona un raytracer. Por eso me he planteado explicarlo más despacio.

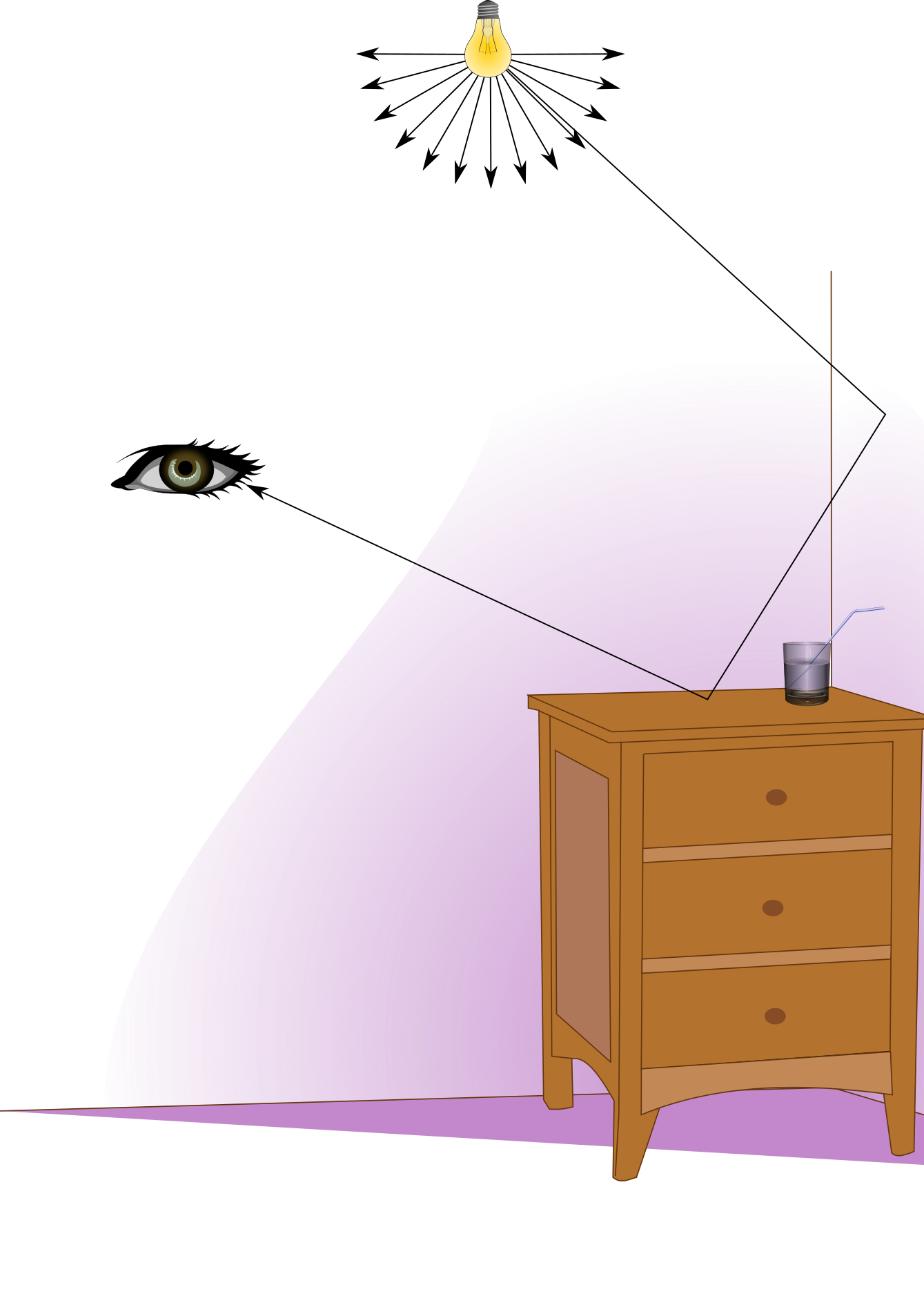
Cuando hablaba, en el artículo anterior, de imitar la luz al revés me refería a que en la vida real, la luz que nos llega al ojo es una parte infinitesimal de la que parte de las fuentes de luz. Los fotones rebotan azarosamente sobre los objetos y algunos de ellos, muy pocos, llegan a nuestros ojos. El color lo marca la longitud de onda que llega a nuestros receptores, es decir: la que los objetos no hayan absorbido durante el camino de esa luz.

Programar un sistema que utilice el mismo procedimiento es prácticamente imposible: habría que simular miles de millones de rayos para seleccionar el color sólo de los que llegan al receptor. Quizá la computación cuántica llegue a tal nivel de proceso, pero de momento es inalcanzable.

Así pues lo que se hace es simular el «camino de vuelta» de los rayos que nos interesan: los que llegan al receptor. Sin duda, es un planteamiento más sencillo de acometer aunque no tan sencillo como parece explicado de primeras. La pregunta es: ¿de qué color tengo que pintar un pixel determinado? Parece una pregunta fácil, pero la respuesta es compleja.

El color de un pixel dependerá no sólo del material del objeto, acordaos de nuestra primera esfera dibujada:

Como veis, la esfera es absolutamente plana, lo que nos permitiría percibir su forma sería la diferente orientación de su superficie con respecto a la fuente de luz; también dependería el color de la luz reflejada y refractada que hay en el «mundo» y de las sombras que puedan proyectar otros objetos. Repito: cuando enviamos desde la cámara unos rayos de color cuya finalidad es averiguar qué color tendrá el pixel determinado sabemos que ese color dependerá también del color de la luz reflejada por otros objetos a su alrededor y si ha alcanzado algún objeto transparente, también dependerá de la refracción que tenga ese rayo y del color del objeto visto a través y así un largo etcétera.

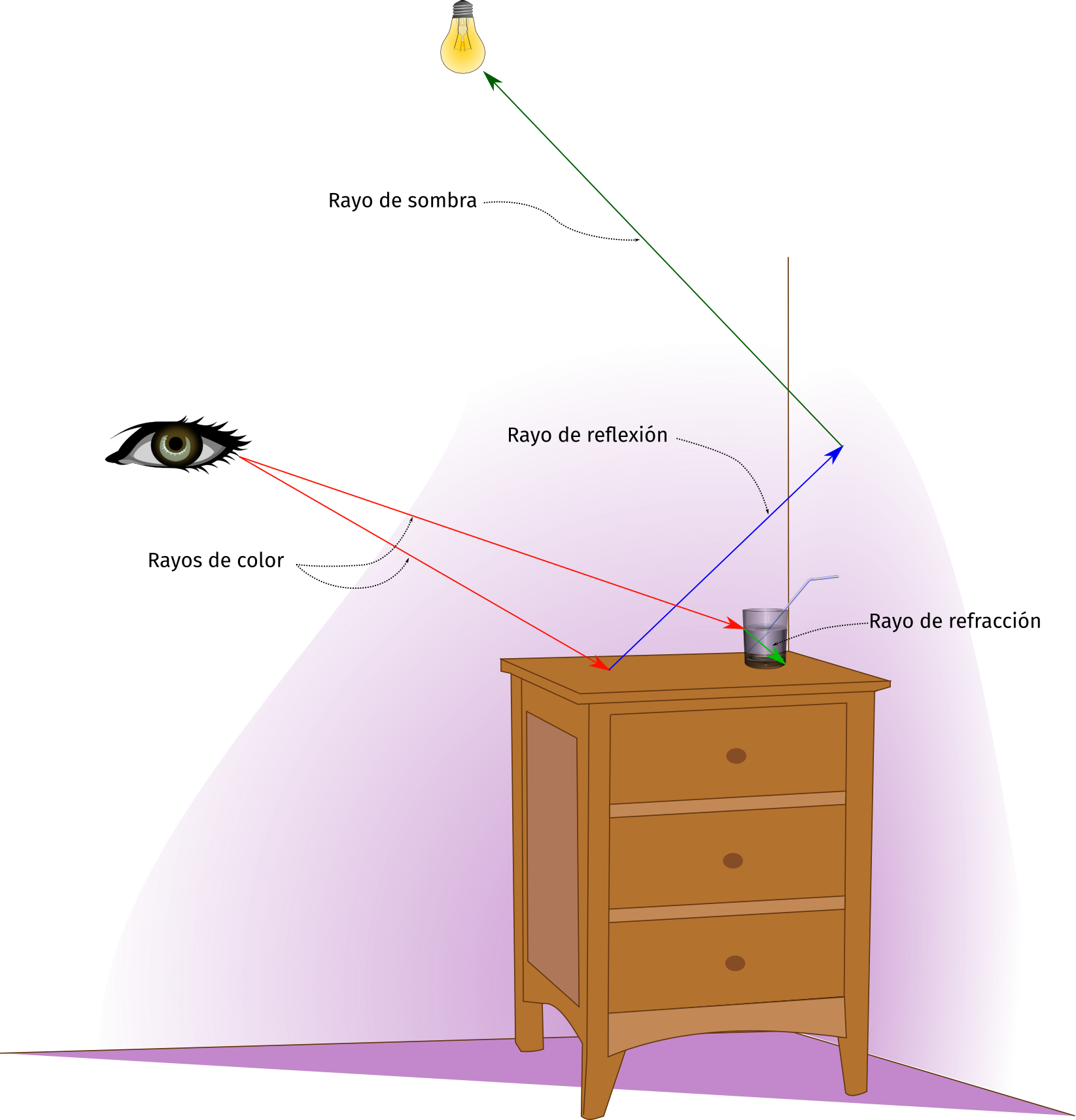
En la otra figura anterior he dibujado algunos de los rayos que un raytracer utiliza en sus cálculos:

• Rayo de color es aquel que se lanza desde el punto de vista para obtener qué color tendrá el pixel de la imagen final. Depende del material del objeto con el que choque y de su orientación hacia la luz.
• Rayo de reflexión modifica el color del punto alcanzado por el rayo de color. Sabemos que hay materiales que reflejan más su entorno que otros: sin llegar al extremo del espejo, compara un metal pulido con una goma de borrar.
• Rayo de sombra se traza para averiguar la cantidad de luz que llega al punto alcanzado por el rayo. Si hay objetos que se interpongan a esa luz y si la superficie está o no orientada hacia la fuente.
• Rayo de refracción es aquel que se traza cuando se alcanza un objeto transparente. Todos hemos observado cómo la luz se desvía al atravesar un vaso de agua y por tanto, el raytracer debe hacer lo mismo si quiere ser realista.

Pero todo esto son complicaciones que nos iremos encontrando cuando el sistema avance más de estos primeros balbuceos en los que nos encontramos.

En estos días, desde el último artículo, no he avanzado en el contenido del libro y me he centrado más en aspectos de cómo traducir todo el sistema a erlang. El código ha sufrido una profunda refactorización. En realidad debería decir refactorizaciones porque en estos días he hecho dos. La primera no me gustó, porque no me aportaba nada de aprendizaje sobre erlang. Era montar una aplicación tocha, con supervisores y procesos apoyándome en OTP². Llegué incluso a rehacer todo el código para dibujar nuestra esfera sin ningún problema y fue tan sencillo que me dije: no he aprendido nada.

Como soy tendente a complicarme yo sólo la vida, pensé: ¿qué pasa si lo hago a mi manera, a las bravas? ... por supuesto, en ello estoy, complicándome la vida. Entre otras cosas porque me tropecé con un error que se me hizo muy difícil de encontrar y me costó trazar nuestra esfera. Finalmente, con la ayuda del amigo deesix lo encontramos. Problemas por mi falta de fluidez con erlang. El resumen de la búsqueda del bug era que repasé centenares de veces la fórmulas y los cálculos que hacían las fórmulas. En algunos casos llegué a hacer los cálculos con papel y lápiz, ─y mucha goma de borrar─, para comprobar si un determinado valor estaba siendo calculado correctamente. Y sabía que estaba rondando la cámara virtual, pero tardé en encontrarlo. Al final, la ayuda del amigo Deesix fue determinante para encontrarlo y era un problema de asignación de valores a una variable.

Los libros que voy siguiendo³ a estas alturas comienzan a derivar clases y utilizar otras características de C++ que desde erlang no tiene sentido seguir, así pues, para estos problemas no son una referencia. Quería aprender, y de momento estoy aprendiendo un montón sobre cómo funciona erlang y lo potente que es. Sin embargo, estoy aprendiendo por la vía dura de darme cabezazos casi constantemente, más contra mi falta de habilidad que contra la complejidad del mismo sistema. El objetivo buscado era conseguir lanzar todos los rayos para la imagen básica... la repito aquí para saber a qué nos referimos:

Bueno, pues básicamente me planteé hacer tres procesos:

• Imagen: que inicia el render, almacena la imagen en sus pasos intermedios y la escribe a disco al finalizar.
• Cámara: lanza los rayos desde su punto de origen hacia el mundo que determina el color del rayo. Hay un proceso por rayo... en la imagen que estamos generando son \(400 \times 225 = 90.000\) procesos independientes.
• Mundo: almacena una lista de los objetos que lo forman y se la envía a los procesos de los rayos para que comprueben si chocan con ellos.

Lo interesante de estas cosas de los procesos de erlang es que te dan automáticamente el procesado en paralelo, y eso también tuvo algunas consecuencias que mi lógica lineal no consiguió atrapar a la primera.

Por ejemplo, hasta ahora no hacía falta almacenar la información de cada pixel pues se procesaban uno tras otro y se escribían directamente en su correspondiente fichero. Tuve que hacer algunos cambios y ahora la imagen se guarda en memoria en un diccionario indexado por el valor del pixel. El código de la función principal que veníamos trabajando quedó así:

dibujar(Estado) ->
    io:format("Iniciando dibujo...~n"),

    %% Datos de la Imagen
    #state{ancho=Ancho,alto=Alto} = Estado,
    io:format("Establecidos datos de la imagen...~n"),

    %% Render
    lists:map(
      fun(J) ->
              io:format("."),
              lists:map(
                fun(I) ->
                        U = I / (Ancho - 1),
                        V = J / (Alto - 1),
                        UV = {U,V},
                        Pixel = {I,J},
                        camara ! {trazar_rayo,Pixel,UV}
                end,
                lists:seq(0, Ancho - 1))
      end,
      lists:seq(Alto - 1, 0, -1)),
    io:format("\nFinalizado\n").

Como veis el bucle lo único que calcula es el pixel y el UV para mandárselo a la cámara y se olvida de todo lo demás. Para volcar la imagen hice otra función que se llama aparte:

escribir_imagen(Estado) ->
    #state{ancho=Ancho,alto=Alto,lienzo=Lienzo} = Estado,
    Cabecera = io_lib:format("P3~n~p ~p~n255~n", [Ancho,Alto]),
    Imagen =
        lists:map(
          fun(J) ->
                  io:format("."),
                  lists:map(
                    fun(I) ->
                            Color = maps:get({I,J}, Lienzo, {1,0,1}),
                            rerl:escribe_color(Color)
                    end,
                    lists:seq(0, Ancho - 1))
          end,
          lists:seq(Alto - 1, 0, -1)),
    {ok, F} = file:open(Estado#state.fichero, [write]),
    file:write(F, Cabecera ++ Imagen),
    file:close(F),
    io:format("\nFinalizado\n").

De esta función, cabe llamar la atención al color por defecto que se empleará en el caso de que algún determinado pixel no se encuentre en el diccionario que guarda la imagen: {1,0,1}. Elegí poner un valor por defecto por dos razones:

1. Pensé que se me perdían algunos rayos y me adelanté a que en imágenes más complejas no pudiera distinguir el negro de falta un pixel del negro generado por el cálculo. El ojo humano no es perfecto y darse cuenta de errores de pérdida de rayos por el color va a ser complicado... sobre todo si utilizas un color tan habitual como el negro.
2. No hubiera puesto ningún valor por defecto si hubiera estado seguro de que se dibujaban todos los rayos.

Esto fue porque me llevé el primer susto cuando tenía ya todo preparado para que empezara a funcionar de manera paralela. Lancé el procedimiento y ese lanzamiento fue paralelo⁴. Obtuve una imagen tal que:

¿Cómo? ¿No ha dibujado nada?, pensé. Y empecé a repasar el código una y otra vez... si ésto debería funcionar. No encontrando el fallo le puse algunos mensajes de aviso que me informaban si el proceso pasaba por algunas determinadas funciones o no. Me di cuenta de que además esos mensajes llegaban en un orden casi aleatorio, para obtener una imagen tal que:

La conclusión fue sencilla después de que el lelo se diera cuenta del para y de que el pobre proceso mundo estaba trabajando como podía cuando los demás ya habían dado por concluida la jornada laboral. Los procesos cámara e imagen estaban en total reposo mientras el pobre mundo iba sacando el higadillo para poder terminar antes de que yo cortara el proceso creyéndolo acabado. La solución de momento es ponerle un contador a la cámara y que controle cuantos rayos se han lanzado. Cuando el proceso mundo le manda el color de un pixel a imagen, ésta informa a la cámara de que actualice el contador de rayos sueltos. De esta manera se obtuvo la imagen esperada:

En el futuro quizá haya que automatizar el proceso de generar la imagen de otra manera, teniendo claras las circunstancias en las que se puede dar por concluido el procesamiento, pero de momento, como el contador funciona y es simple de entender hasta para una mente tan obtusa como la mía, pues lo mantengo.

Viendo el chasco con este primer intento por paralelizar los cálculos, me decidí a convertirlo todo en procesos al más puro estilo erlang, hasta los rayos. En realidad, si miramos el código, el proceso del rayo está preparado para perpetuarse en un bucle, pero se mantiene sólo hasta haber escrito el pixel. Sin embargo, no estoy seguro, pero creo que será útil que se perpetúe durante un tiempo si ha de lanzar otros rayos desde él: rayos de sobra, o de reflexión, o de refracción o antialiasing y esperar a tener una respuesta con un color más preciso.

start(R, Pixel, UV) ->
    spawn(?MODULE, init, [#state{rayo=R,pixel=Pixel,uv=UV}]).

init(State) ->
    self() ! impacto,
    loop(State).

loop(State) ->
    receive
        impacto ->
            impacto(State, 0, ?INFINITO);
        _ ->
            loop(State)
    end.

%%-------------------------------------------------------------------------
%% Funciones privadas
%%-------------------------------------------------------------------------

color(Objeto, R, Tmin, Tmax) ->
    Hay_impacto = rerl_objeto:impacta(Objeto, {R,Tmin,Tmax}),
    case Hay_impacto of
        {true,Np} ->
            {X,Y,Z} = Np,                                  % normal en el punto
            rerl:mul({X+1,Y+1,Z+1}, 0.5);                  % usar coordenadas como {R,G,B}
        false ->
            {_,Y,_} = rerl:vector_unidad(R#rayo.dir),
            T = 0.5 * (Y + 1),
            rerl:suma(rerl:mul({1.0,1.0,1.0}, (1-T)),      % Del color blanco {1,1,1}
                      rerl:mul({0.5,0.7,1.0},  T));        % al color azul {0.5,07,1.0}
        _ ->
            {1,0,0}
    end.

impacto(Estado, Tmin, Tmax) ->
    mundo ! {self(), {get_objetos}},
    Objetos =
        receive
            {_, Respuesta} ->
                Respuesta
        end,
    #state{rayo=R,pixel=Pixel} = Estado,
    Impactos =
        lists:map(
          fun(Obj) ->
                  color(Obj, R, Tmin, Tmax)
          end,
          Objetos),
    Color = hd(Impactos),
    imagen ! {pixel_color,Pixel,Color}.

El problema se arregló como dije, con ayuda. Me repasé las fórmulas sienes y sienes de veces sin encontrar el error, las deconstruí realizando los cálculos paso a paso y aún así la cámara seguía sin enfocarse. Cuando se encontró el error fue el momento para perseguir el objetivo inmediato que sigue el libro: diferenciar la cara interna de la externa de los objetos.

Además, también, contaros cómo se ha conseguido representar varios objetos en la escena, siguiendo el espíritu del libro, pero con un código que se parece al original aún menos de lo que venía pareciéndose hasta ahora.

El tema comienza con el registro impacto:

-record(impacto, { p            = {0,0,0}    % vec3:     Punto del impacto
                 , normal       = {0,1,0}    % vec3:     Normal en el punto del impacto
                 , t            = 0          % Num:      Factor de distancia del impacto
                 , cara_frontal = false}).   % Booleano: define si es impacto externo

Ese registro está preparado para devolver toda la información que necesita el sistema para calcular el color. Echo de menos el mismo registro de color en él, pero supongo que al no tener todavía ningún tipo de soporte para texturas no lo necesita.

Básicamente consiste en determinar si el rayo coincide con la superficie desde el interior o desde el exterior y cuál es la normal en ese punto:

Para ver si está impactando en una cara desde el exterior se utiliza la función:

cara_frontal(Rayo, Impacto, Normal) ->
    Cara_Frontal = punto(Rayo#rayo.dir, Normal) < 0,
    N =
        case Cara_Frontal of
            true -> Normal;
            false -> mul(Normal, -1)
        end,
    Impacto#impacto{cara_frontal=Cara_Frontal,normal=N}.

Básicamente, como se puede ver es que comprueba el ángulo que forman el rayo y la normal en el punto. Si están enfrentados es una cara externa y en caso contrario interna (y le damos la vuelta a la normal).

También es importante saber en qué punto(s) se produce ese impacto. Hay que recordar que en nuestro modelo una esfera es sólo una fórmula matemática y por tanto esos puntos no tienen grosor. Además de que lo más probable es que si hay impacto con un objeto 3D no sea único sino que atraviese el objeto al menos en dos puntos⁷.

Ese registro se genera en el objeto, concretamente en la función hay_impacto/4:

hay_impacto(#esfera{centro=Centro,radio=Radio}, #rayo{origen=Origen,dir=Dir}=R, Tmin, Tmax) ->
    OC = rerl:resta(Origen, Centro),
    A = rerl:modulo_cuadrado(Dir),
    Medio_B = rerl:punto(OC, Dir),
    C = rerl:modulo_cuadrado(OC) - (Radio * Radio),
    Discriminante = (Medio_B * Medio_B) - (A * C),
    if
        Discriminante > 0 ->
            Raiz = math:sqrt(Discriminante),
            T1 = (-Medio_B - Raiz) / A,
            if
                T1 < Tmax andalso T1 > Tmin ->
                    T = T1,
                    P = rerl:hacia(R, T),
                    Normal = rerl:dividir(rerl:resta(P, Centro), Radio),
                    Impacto = #impacto{p=P,t=T,normal=Normal},
                    Exterior = rerl:cara_frontal(R, Impacto, Normal),
                    {true, Impacto#impacto{cara_frontal=Exterior}};
                true ->
                    %% Este choque debería ser tenido en cuenta como impacto de salida
                    %% entiendo que en el libro lo obvia porque aún no hay materiales
                    %% trasparentes y sólo lo tiene en cuenta si falla el anterior.
                    T2 = (-Medio_B + Raiz) / A,
                    if
                        T2 < Tmax andalso T2 > Tmin ->
                            T = T2,
                            P = rerl:hacia(R, T),
                            Normal = rerl:dividir(rerl:resta(P, Centro), Radio),
                            Impacto = #impacto{p=P,t=T,normal=Normal},
                            Exterior = rerl:cara_frontal(R, Impacto, Normal),
                            {true, Impacto#impacto{cara_frontal=Exterior}};
                        true ->
                            {false, #impacto{t=?INFINITO}}
                    end
            end;
        true ->
            {false, #impacto{t=?INFINITO}}
    end;
hay_impacto(_,_,_,_) ->
    geometria_desconocida.

Como se puede apreciar se generan impactos, bueno, en realidad se genera sólo uno, ─o ninguno─. En el caso de que no haya impacto se devuelve una tupla {false,#impacto{t=?INFINITO}}. Esto sirve, para que el rayo pueda ordenar por distancia los impactos que haya:

impacto(Estado, Tmin, Tmax) ->
    mundo ! {self(), {get_objetos}},
    Objetos =
        receive
            {_, Respuesta} ->
                Respuesta
        end,
    #state{rayo=R,pixel=Pixel} = Estado,
    %% Obtener todos los impactos del rayo con objetos
    Impactos =
        lists:map(
          fun(Obj) ->
                  rerl_objeto:impacta(Obj, {R,Tmin,Tmax})
          end,
          Objetos),
    %% Ordenarlos de más cercano a más lejano
    Iorden =
        lists:sort(
          fun(I,J) ->
                  {_,#impacto{t=T1}} = I,
                  {_,#impacto{t=T2}} = J,
                  T1 < T2
          end,
          Impactos),
    Color = color(Estado,hd(Iorden)),
    imagen ! {pixel_color,Pixel,Color}.

Esta función obtiene una lista de objetos en el mundo y establece si se cruza con ellos. Esos Impactos luego se ordenan en Iorden y se obtiene el Color más cercano.

De momento, también, ese color lo decide el rayo sin embargo, me parecería más lógico que lo decidiera el objeto o la textura.

La imagen obtenida es:

Os recuerdo los datos con los que se generan ambas esferas:

{esfera,{0,0,-1},0.5}.
{esfera,{0,-100.5,-1},100}.

Nuestra esfera de siempre es la que tiene centro en {0,0,-1} y un radio 0.5. La otra se puede observar que tiene un radio 100 y se sitúa su centro en {0,-100.5,-1}. Es decir, esta segunda se sitúa justo debajo de nuestra esfera de siempre a -100.5 en la coordenada y. 100 de su propio radio y 0.5 de la otra. Por tanto, sabemos que ambas están situadas una encima de la otra y apenas se tocan en un solo punto.

Si vemos la esfera inferior de color verde mientras la pequeña la vemos azul es por el tema de las normales. Como sabéis se está utilizando como color el valor de la normal en el punto. Mientras a la pequeña la vemos desde un lateral orientado en el eje z, a la grande la vemos desde la parte superior, orientada con el eje y. Puesto que pasamos los valores de {x,y,z} directamente a valores {r,g,b} los orientados en y se mapean a g y los orientados a z se mapean a b. También podemos ver que la parte derecha de la esfera pequeña es más rojiza que la izquierda, puesto que en horizontal el componente que se alinea es x que se mapea a r.

También le añadí un contador de tiempos a la imagen, desde el momento en se que lanza hasta el momento en que se guarda la imagen a archivo. Con este contador he conseguido averiguar algunas cosas interesantes sobre el procesado paralelo de la generación de imagen. Por ejemplo, lanzando 10 procesos y lanzando 100 he encontrado que el tiempo final del render no varía mucho. Ambos valores sobrepasan la capacidad de hilos que puede dar la máquina y lo que obtienes al final es un montón de procesos parados esperando su turno para ejecutarse. Eso sí, cuantos más procesos más memoria se gasta. No es muy importante con dichas cantidades, que pueden variar entre los 0,8Kb y 1,3Mb, pero cuando lanzas 100 procesos por pixel, puede llegar a desbordar la memoria y bloquear la máquina.

Tal y como va el sistema ahora, con 100 muestras (samples) por pixel, una imagen sencilla como la que está generando el proceso tarda, en mi máquina, que ya tiene sus añitos, alrededor de minuto y medio. Puede parecer mucho, sobre todo porque sin el refinado de las muestras tarda apenas un par de segundos. Sin embargo, por comparar veamos las dos imágenes juntas:

Ya sé que el artículo de hoy ha sido un poco ladrillo y parece que avanza poco en el objetivo. Pero... De momento tengo un sistema que funciona con procesos paralelos. No está afinado, todavía tengo que afinarlo más. Los planes, de momento, son eliminar los procesos de los objetos y el mundo para que los procesos de render por teselas no tengan que estar llamando a sólo unos pocos procesos desperdiciando un poco la paralelización del procedimiento. Es decir, que los datos sean accesibles para todos de manera directa sin estar enviando llamadas al mismo proceso creando un embudo o cuello de botella. Por otro lado, seguramente los procesos de imagen, cámara y controlador terminen unificados. Sin embargo, mis planes siguientes es avanzar un poco más en el tutorial del libro y abandonar un poco el de los procesos. No por olvidarlos sino por no saturarme con el cómo dejando de lado el qué. Seguramente haya algún avance más que se pueda llevar a cabo en la generación de imágenes para ir, poco a poco, avanzando también en el cómo más adelante. Además, conociendo mejor el sistema y las necesidades que irá generando, y otras que me gustaría ir probando: como por ejemplo, si consigo que el proceso paralelo se pueda distribuir por una red de ordenadores de forma sencilla y aumentar así la velocidad en la que se pueden realizar las imágenes.

De ahí a montar una granja de render hay un abismo, pero sería uno de los objetivos que me gustaría aunque no sea más que esbozar y poder tener dos o tres máquinas generando la misma imagen y aprender cómo se puede controlar un proceso distribuido como ese.

Me gustaría también, en un futuro, toquetear el tema de los diferentes ficheros de entrada. Hacer, por ejemplo, que pudiera interpretar diferentes datos que provengan de, por ejemplo, povray, renderman, vray, etc.; además de su propio sistema. Y, por último, también me gustaría explorar la vía de hacer algún plugin para Blender3D o, aprovechando que chufla también en erlang, para Wings3d... pero para estas cosas, primero hay que terminar lo básico.