La cámara de los rayos sin truenos
Pues sigo con los apuntes de raytracing, ya me perdonaréis el
cansinamiento pero el libro éste y el picar código porque sí y no
por trabajo o necesidad, me está resultando gratificante. Quizá a
alguien que pueda leer ésto y no esté familiarizado con estas cosas
puede resultarle un poco árido: ¡Uff! A estas alturas hablando de matemáticas y programación con erlang. ¡Qué ganas de marear la perdiz! Pues sí, quizá ese pensamiento sea correcto y hasta cierto,
según el punto de vista que se adopte, claro. En mi caso, ya lo
sabréis si leísteis el artículo anterior, es una forma de procrastinar
aprendiendo algo inútil para mi vida profesional, pero que llena de
orgullo y satisfacción mi yo más friki.
Después del artículo del otro día algunos lectores me han pedido el código que voy haciendo. Por ello he decidido compartir el código que vaya escribiendo en repositorio público en codeberg.org. Además, otro par de lectores me han dicho que están más interesados en el concepto, en la explicación teórica que subyace en estas herramientas, más que en el código. Así pues, he decidido incluir también un poco de matemáticas y otras explicaciones. No demasiadas, sólo las suficientes para que las cosas queden más o menos claras. Ya conocéis mi natural tendencia a pichorros y chismáticos y quizá mi explicación no sea tan rigurosa como a algunos les gustaría, pero esta vez intentaré ser algo más preciso si es posible.
Lo primero es explicar un poco qué es un raytracer y por qué consigue imágenes tan realistas. Y lo hace tan bien porque intenta emular cómo funciona la luz en la vida real. Lo imita, pero dándole la vuelta, es decir, en lugar de seguir la luz desde la fuente de luz hasta rebotar en los objetos que correspondan y llegar hasta el ojo, lo que hace es trazar ese camino desde el ojo hasta los objetos y luego a las fuentes de luz. ¿Por qué lo hace al revés? Pues básicamente porque no se puede lanzar los millones de millones de fotones que lanza una fuente de luz para que sólo unos pocos cientos de ellos lleguen a estimular el ojo durante ese mismo lapso de tiempo. Por eso es más efectivo y rentable trabajar sólo con los fotones que llegan en lugar de con los que salen de las fuentes de luz.
La cámara de los rayos sin truenos
El concepto de rayo es muy simple: es una recta con dirección. Con un dibujo quedará más claro:
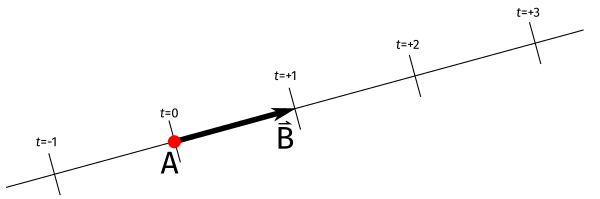
Una recta en el espacio 3D se puede definir como aquella línea que
pasa por dos puntos. Un rayo se apoya en esa recta, tomando como
origen uno de esos puntos. Por tanto, un rayo es una semi-recta:
puesto que una línea es infinita sin principio ni fin, el rayo sería
su mitad, tiene principio en origen y continúa en la recta apoyado
pasando por el otro punto que llamamos dirección (en el código
dir). La fórmula matemática es \(\mathrm{P}(t)=\mathrm{A}+t\mathrm{b}\)
y como se puede ver en el dibujo, \(t\) permite desplazar el punto a lo
largo de toda la recta. Dicha fórmula se vuelca en el código en la
función rayo:hacia/2:
hacia(R,T) -> vec3:suma(R#rayo.origen, vec3:mul(R#rayo.dir,T)).
Bueno, vale, ya tenemos rayos que podemos trazar, con su origen, su dirección y su correspondiente fórmula para trazarse. Es el momento de recordar cómo funciona un raytracer. El proceso es muy sencillo:
- Calcular el rayo que va desde la cámara al pixel.
- Determinar los objetos con los que tiene intersección.
- Según esas intersecciones, calcular el color del pixel.
- Repetir para todos los pixels de la imagen.
La cámara es otra abstracción. En el libro la coloca en el punto
(0,0,0). A partir de ese punto origen se trazarán los rayos hacia
los distintos pixels situados en el viewport, cuyo centro será el
(0,0,-1). Como se puede ver en la imagen, el eje \(x\) estará
orientado horizontalmente, el eje \(y\) verticalmente y el \(z\) nos dará
la profundidad. Veamos el gráfico:

Si suponemos que el origen de coordenadas está situado en nuestra pantalla del ordenador, el eje \(y\) crece hacia arriba, el \(x\) hacia la derecha y el \(z\) hacia nosotros y decrece alejándose. El objetivo del libro es conseguir la siguiente imagen de fondo trazando rayos:

Repasamos el código
Modificaciones al código del libro
Adaptando el código a erlang he modificado algunas cosas para
conseguir el mismo resultado.
Rayo
En registros.erl se añade un record para los rayos y también el
correspondiente módulo.
-record(rayo, {origen, dir}).
-module(rayo). -include("registros.hrl"). -export([nuevo/2]). nuevo(Origen,Direccion) -> #rayo{origen=Origen, dir=Direccion}. hacia(R, T) -> vec3:suma(R#rayo.origen, vec3:mul(R#rayo.dir, T)).
De momento no hace falta comentar mucho más, veamos el código que genera la imagen.
Imagen
color_rayo(Rayo) -> DU = vec3:unidad(Rayo#rayo.dir), T = 0.5 * (DU#vec3.y + 1), color:suma(color:mul(color:nuevo(1.0,1.0,1.0), 1-T), color:mul(color:nuevo(0.5,0.7,1.0), T)).
Como antes dije, hay que calcular el color que tiene el rayo lanzado. Esto lo hace la función anterior. Realmente lo que hace es mezclar blanco y azul dependiendo de la altura. La fórmula que se emplea para hacer la mezcla es la siguiente:
\[Color_{mezcla} = (1-t) \cdot Color_{inicial} + t \cdot Color_{final}\]
Los valores inicial y final son el blanco rgb(1,1,1) y el azul
rgb(0.5,0.7,1.0). El valor lo determina el componente \(y\). Se
obtiene la dirección del rayo se distribuye el valor T uniformemente
de abajo a arriba. Cuando T tiene a 1 el color blanco tiende a
desaparecer y cuando tiende a cero, es el azul el que lo hace.
dibujar(Fichero) -> %% Imagen Ratio = 16 / 9, Ancho = 400, Alto = round(Ancho / Ratio), %% Cámara Alto_Vista = 2, Ancho_Vista = Ratio * Alto_Vista, Foco = 1, Origen = vec3:nuevo(0,0,0), Horizontal = vec3:nuevo(Ancho_Vista, 0, 0), Vertical = vec3:nuevo(0, Alto_Vista, 0), Esquina_Inferior_Izquierda = vec3:resta( vec3:resta( vec3:resta(Origen, vec3:divi(Horizontal,2)), vec3:divi(Vertical,2)), vec3:nuevo(0,0,Foco)), %% Render Cabecera = io_lib:format("P3~n~p ~p~n255~n", [Ancho,Alto]), {ok,F} = file:open(Fichero, [write]), Imagen = lists:map( fun(J) -> io:format("Faltan ~p filas \e[36D", [J]), lists:map( fun(I) -> U = I / (Ancho - 1 ), V = J / (Alto - 1), Punto = vec3:resta( vec3:suma( vec3:suma( Esquina_Inferior_Izquierda, vec3:mul(Horizontal,U)), vec3:mul(Vertical, V)), Origen), R = rayo:nuevo(Origen, Punto), Color = color_rayo(R), color:escribe(Color) end, lists:seq(0,Ancho)) end, lists:seq(Alto,0,-1)), file:write(F, Cabecera ++ Imagen), file:close(F), io:format("\nFin.\n").
Si vemos el código, lo único que necesita un poco de explicación es la
creación del rayo. Como vemos el rayo se crea con origen en el
Origen de la cámara hasta el Punto.
\[Punto = EsquinaInferiorIzquierda + U \cdot Horizontal + V \cdot Vertical - Origen\]
Los valores U y V están representados en el esquema gráfico de la cámara.
Dibujando la primera esfera
Hasta aquí todo muy bonito, pero hemos venido a dibujar cosas y lo más socorrido es un esfera. Calcular una esfera es sencillo: necesitas sólo las coordenadas del centro y un radio. Es decir, siendo un poco más preciso cumple con la siguiente fórmula: \(x^2 + y^2 + z^2 = R^2\).
Cómo es una esfera (aparte de redonda)
Otra historia es saber si un punto dado está dentro o fuera de la esfera. Pero es sencillo, si dadas sus coordenadas \((x,y.z)\) cuando \(x^2 + y^2 + z^2 > R^2\) y estará dentro si \(x^2 + y^2 + z^2 < R^2\)
Para complicarlo un poco más, necesitamos esa ecuación en formato vectorial. Para ello si el centro de la esfera es \((C_x,C_y,C_z)\) la cosa quedaría así, para cualquier punto en la superficie de la esfera: \[(x-C_x)^2 + (y-C_y)^2 + (z-C_z)^2 = r^2\]
Puesto que podemos escribir el centro como \(\mathrm{C}=(C_x,C_y,C_z)\) y siendo el punto \(\mathrm{P}=(x,y,z)\), podemos escribir que el radio \(r\) es \((\mathrm{P}-\mathrm{C})\). Es decir:
\[(\mathrm{P}-\mathrm{C}) \cdot (\mathrm{P}-\mathrm{C}) = r^2\]
Hasta ahora tenemos la forma de saber qué punto satisface la esfera nos falta saber si un punto satisface también el rayo. Si recordamos, podemos escribir el rayo como \[\mathrm{P}(t) 0 \mathrm{A} + t\mathrm{b}\]. Por lo que un punto que satisfaga la esfera y el rayo a la vez se puede escribir como:
\[(\mathrm{P}(t)-\mathrm{C}) \cdot (\mathrm{P}(t)-\mathrm{C}) = r^2\]
Por lo tanto,
\[(\mathrm{A}+t\mathrm{b}-\mathrm{C}) \cdot (\mathrm{A}+t\mathrm{b}-\mathrm{C}) = r^2\]
y despejando todo, encontramos una ecuación de segundo grado:
\[t^2 \mathrm{b} \cdot \mathrm{b} + 2 t \mathrm{b} \cdot (\mathrm{A} - \mathrm{C}) + (\mathrm{A} - \mathrm{C}) \cdot (\mathrm{A} - \mathrm{C}) - r^2 = 0\]
Básicamente, por tanto, hay que resolver una ecuación de segundo grado
\[t = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]
Los posibles resultados son:
- No existe ninguna solución válida para la ecuación. En este caso el rayo no incide en la esfera.
- Existe una solución única. En este caso el rayo es tangente a la esfera y sólo cumple la ecuación en un punto.
- Existen dos soluciones. En este caso el rayo atraviesa la esfera y hay un impacto de entrada con orificio de salida.
El código
Muy bonitas las matemáticas, parezco intelectual poniendo un par de fórmulas. Ahora hay que traducirlo a código. La imagen que buscamos es:

Como el código de dibujar se repite1 y en todo caso lo podéis
descargar del repositorio. Pondré el código de la función implica la
resolución de la esfera que lo llamará la función color_rayo/1:
en_esfera(Centro, Radio, Rayo) -> OC = vec3:resta(Rayo#rayo.origen, Centro), A = vec3:punto(Rayo#rayo.dir, Rayo#rayo.dir), B = 2.0 * vec3:punto(OC, Rayo#rayo.dir), C = vec3:punto(OC,OC) - Radio*Radio, Discriminante = B*B - 4*A*C, Discriminante > 0. color_rayo(Rayo) -> Dis = en_esfera(vec3:nuevo(0,0,-1), 0.5, Rayo), case Dis of true -> color:nuevo(1,0,0); false -> DU = vec3:unidad(Rayo#rayo.dir), T = 0.5 * (DU#vec3.y + 1), color:suma(color:mul(color:nuevo(1.0,1.0,1.0), 1-T), color:mul(color:nuevo(0.5,0.7,1.0), T)) end.
Como se puede apreciar, la función en_esfera/3 resuelve la ecuación
de segundo grado y determina si tiene una o más soluciones. La función
color_rayo/1 se ha modificado para devuelva el color rojo de la esfera
con color:nuevo(1,0,0) o en caso contrario devuelva el color de
fondo que corresponda.
Dibujando normales
Lo que es un vector normal
El vector normal es un vector de módulo uno orientado de forma perpendicular a una superficie. Dicho con otras palabras es un vector que va «hacia afuera» de la superficie. Por ejemplo, en la esfera quedaría más o menos así:

O dicho de otro modo si la esfera fuera la Tierra y te pones en pie, tus pies estarán en el punto de la superficie terrestre y tu cabeza sería «la flechita» de la punta.
¿Por qué son importantes? Pues porque nos indican hacia dónde están orientadas las superficies.
Las normales afectan al color
Como acabo de decir, las normales indican hacia dónde está orientada la superficie, de manera que percibimos la forma del objeto porque unas zonas reciben más luz que otras según estén más orientada hacia la luz o no. Por eso, nuestro dibujo ha resultado plano, porque cuando el rayo incidía en la esfera el color era siempre el mismo \((1,0,0)\).
Si cambiamos un poco el código y convertimos el color según la normal al punto, con un poco de código adicional, modificando el cálculo de la intersección del rayo con la esfera y color que se devuelve, tal que:
en_esfera(Centro, Radio, Rayo) -> OC = vec3:resta(Rayo#rayo.origen, Centro), A = vec3:punto(Rayo#rayo.dir, Rayo#rayo.dir), B = 2.0 * vec3:punto(OC, Rayo#rayo.dir), C = vec3:punto(OC,OC) - (Radio*Radio), Discriminante = (B*B) - (4*A*C), if Discriminante < 0 -> -1; true -> (-B - math:sqrt(Discriminante)) / (2.0*A) end. color_rayo(Rayo) -> R = en_esfera(vec3:nuevo(0,0,-1), 0.5, Rayo), if R > 0 -> N = vec3:unidad(vec3:resta(rayo:hacia(Rayo,R),vec3:nuevo(0,0,-1))), color:mul(color:nuevo(N#vec3.x+1,N#vec3.y+1,N#vec3.z+1),0.5); true -> D = vec3:unidad(Rayo#rayo.dir), T = 0.5 * (D#vec3.y + 1), color:suma(color:mul(color:nuevo(1.0,1.0,1.0), 1-T), color:mul(color:nuevo(0.5,0.7,1.0), T)) end.
Veamos la imagen que obtenemos con esos pequeños cambios:

Si habéis trabajado con Blender3D o con otros programa similares os sonará el concepto de normals field o campo de normales. Una imagen, que aplicada después a un objeto, modifica las normales del mismo haciéndolo más detallado. Es un truco muy habitual para dar detalle a un objeto con pocos polígonos:
- Se crea un objeto muy detallado con incluso millones de caras si se quiere.
- Se genera un campo de normales.
- Se simplifica el modelo hasta dejarlo en unos pocos cientos de caras.
- Se aplica el campo de normales como textura consiguiendo con un modelo lowpoly la apariencia detallada que se busca.
Bien, eso es lo que hemos hecho con ese código: visualizar el campo de normales de la esfera como si fuera una textura de color.
En el libro, a continuación proponen una simplificación de los cálculos. Ahorran un par de multiplicaciones y divisiones, pero teniendo en cuenta que para generar una imagen de tamaño regular, los rayos trazados pueden ser miles, cientos de miles e incluso millones, lo que están ahorrando pueden ser millones de multiplicaciones y divisiones. Me iba a ahorrar la explicación matemática, pero debido a algunas peticiones de lectores, lo pongo también. Si te lo quieres ahorrar te lo puedes saltar.
Lo que hace el autor es simplificar un poco la fórmula de resolución de ecuaciones de segundo grado sustituyendo el término \(b\) por \(2h\), es decir,
\[\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]
pasa a ser,
\[\frac{-2h \pm \sqrt{(2h)^2 - 4ac}}{2a}\]
Sacando el \(4\) de la raíz quedaría
\[\frac{-2h \pm 2 \sqrt{h^2 - ac}}{2a}\]
y simplificando
\[\frac{-h \pm \sqrt{h^2 - ac}}{a}\]
Volcando esto al código, queda:
en_esfera(Centro, Radio, Rayo) -> OC = vec3:resta(Rayo#rayo.origen, Centro), A = vec3:punto(Rayo#rayo.dir, Rayo#rayo.dir), Medio_B = vec3:punto(OC, Rayo#rayo.dir), C = vec3:modulo_cuadrado(OC) - (Radio*Radio), Discriminante = (Medio_B*Medio_B) - (A*C), if Discriminante < 0 -> -1; true -> (-Medio_B - math:sqrt(Discriminante)) / A end.
Los cálculos están simplificados, pero el resultado de la imagen es la misma.
Conclusiones
Apenas llevamos un 27% del primer libro y ya tenemos un raytracer funcionando. Bueno, vale, es muy limitado y sólo dibuja una esfera, además no de forma realista. Pero está funcionando: trazamos rayos y conseguimos una representación correcta.
A partir de aquí, el libro empieza a utilizar algunas características
de la POO más avanzadas y tengo que estudiar cómo hacer lo mismo,
─parecido o no─, con erlang. Porque hasta ahora nos hemos venido
arreglando con los registros o records, pero se mete en temas de
clases virtuales y otras abstracciones que tengo que «abstraer» de
otra manera.
Footnotes:
Bueno, algún bug he arreglado por el camino.


Comentarios