Un artículo introductorio sobre redes neuronales
De aquellos polvos, estos lodos
La culpa de este artículo la tiene Alberto: en el grupo de Telegram que está abierto para hacer comentarios sobre el blog lanzó la siguiente petición, propuesta, cosa no sé muy bien para qué:

Bueno, vale. La respuesta fácil hubiera sido: «no sé nada» y haberme quitado el marrón de encima por la vía de la ignorancia. La respuesta corta, pero sincera, sería: «muy poco». Así que, falto de temas como ando últimamente para el blog, voy a contaros lo poco que sé: sin ánimo de ser exhaustivo y, sobre todo, queriendo ser breve.
Me presentaron las neuronas artificiales y las pandillas que forman allá por el año 1982, cuando se lanzaba al mercado lo que fue lo más parecido a un ordenador personal que hubo en las casas de la época: el Sinclair ZX Spectrum... uff... 38 años nos contemplan. Insisto en los años, porque nos parece que estas cosas de las Inteligencias Artificiales son de ayer mismo, cuando se remontan por lo menos a anteayer.

Aún guardo como «oro en paño» los apuntes de primero de carrera de Fundamentos de Psicología Matemática. Cuando compré aquellos apuntes fotocopiados que nos dejó el profesor en repografía1, empecé a ojearlos en la biblioteca y me llamaron la atención, precisamente, los apartados que luego no veríamos. Quizá, porque el resto del libro era básicamente el contenido que ya había visto en COU2. Al final no vimos nada de aquellos que me parecieron interesantes: nos quedamos en el temario de COU. Muchos de mis compañeros vinieron a la carrera de Psicología habiéndose pasado todo el bachillerato huyendo de las matemáticas y se tropezaron con ella durante toda la carrera: matemáticas en primero, en segundo estadística, en tercero teoría de tests, en cuarto psicología experimental. En fin... el caso es que me quedé con las ganas de avanzar, entre otras cosas en la aplicación del cálculo matricial en las «redes neuronales formales». Pero nací como irredento curioso me lo miré por mi cuenta.
En aquellos apuntes nos hablaban del primer modelo de neurona formal3 de McCulloch y Pitts en 1943. Si alguien ha curioseado sobre el tema le sonarán esos nombres porque es lo básico, pero básico, de este campo.
Intentando imitar el funcionamiento de las neuronas naturales, esos autores establecen los siguientes axiomas divididos en dos grupos:
- Axiomas estructurales
- La neurona es un mecanismo binario. Es decir, puede tener dos estados: activa o inactiva, o dispara o no, o es 1 o es 0.
- Cada neurona tiene una salida conectada a una o más neuronas. O dicho de otro modo: o activa o no a todas las neuronas a las que está conectada.
- Cada neurona puede recibir un número cualquiera de sinapsis excitadoras o inhibidoras.
- Cada neurona tiene un umbral de disparo a partir del cual se la considera activa y si no se alcanza se la considera inactiva.
- Axiomas funcionales
- La neurona puede cambiar de estado en momentos determinados por la acción de las demás neuronas.
- Sean dos neuronas \(a_i\) y \(a_j\) tales que \(a_i\) está conectada con \(a_j\). La neurona \(a_i\) ejercerá una acción excitadora o inhibidora sobre \(a_j\) en el tiempo \(t+1\) sólo si \(a_i\) está activa en el tiempo \(t\).
- Una neurona está activa en el tiempo \(t\) sólo si la suma de las sinapsis inhibidoras y excitadores que recibe en el tiempo \(t\) sobrepasa el umbral de disparo de la neurona.
- Una neurona no hace sinapsis sobre ella misma4.
Críticas
Como concepto básico, dichos axiomas, pueden resultar suficientes. El problema desde mi punto de vista es que tampoco simulan con mucha precisión el funcionamiento de las neuronas... Para empezar, desde el punto de vista de la neurología:
- Todas las neuronas naturales disparan cuando el nivel de excitación supera el potencial mínimo de la membrana, y ese es una valor estable y compartido por todas ellas.
- Todas las neuronas naturales desactivan la electrificación de su membrana si reciben una excitación demasiado potente. Eso las protege de quedar fritas. Cuando se supera un determinado nivel de activación, la membrana de la neurona deja de conducir la electricidad y se convierte en una membrana celular normal, durante unos milisegundos.
- Las neuronas naturales no disparan por turnos en momentos discretos: están funcionando de manera constante y disparan cuando reciben el estímulo suficiente. Una vez han disparado, la membrana queda también sin electrificar en lo que se conoce como periodo refractario.
Vale, es una simulación para conseguir, conceptualmente, un funcionamiento parecido a lo que sería una neurona natural. Sin embargo, esas críticas quedarían en nada, si al menos el modelo fuera lo suficientemente preciso como para conseguir que esa simulación tenga un funcionamiento correcto y completo. Sin embargo, desde el punto de vista del proceso de las redes neuronales nos encontramos con otros problemas.
En las redes neuronales podemos encontrar que las neuronas pueden establecer conexiones al estilo de las puertas lógicas.

Podemos repasar el gráfico anterior con sus tablas lógicas, suponiendo
que establecemos el nivel mínimo de activación a 25 (para todas las
neuronas), vemos que no hay problema simular las puertas lógicas and
y or.
| \(E_1\) | \(E_2\) | \(Y\) | |
|---|---|---|---|
| 20 | 20 | 40 | Activa |
| 20 | 0 | 20 | no activa |
| 0 | 20 | 20 | no activa |
| 0 | 0 | 0 | no activa |
| \(E_1\) | \(E_2\) | \(O\) | |
|---|---|---|---|
| 25 | 25 | 50 | Activa |
| 25 | 0 | 25 | Activa |
| 0 | 25 | 25 | Activa |
| 0 | 0 | 0 | no activa |
Sin embargo, para la puerta lógica de «o exclusivo» es decir, debe estar activa una o la otra, pero no las dos al tiempo, necesitamos el concurso de una neurona auxiliar que quedaría oculta:
| \(E_1\) | \(E_2\) | \(o\) | \(Ox\) | |
|---|---|---|---|---|
| 25 | 25 | -30 | 20 | no activa |
| 25 | 0 | 0 | 25 | Activa |
| 0 | 25 | 0 | 25 | Activa |
| 0 | 0 | 0 | 0 | no activa |
Se ha marcado en el gráfico de manera distinta la sinapsis de la neurona oculta, en azul con el rombo relleno para remarcar que cuando se activa, su peso de sinapsis es negativo. Es decir, cuando las dos neuronas de entrada se activan, además de activar la salida, activan la oculta que al mismo tiempo inhibe la salida.
Dicho de otro modo, aunque en la vida real, las neuronas pueden
simular un circuito xor del mismo modo que lo hace con los otros. Es
decir, no se necesita una tercera neurona en el circuito para que la
puerta lógica funcione.
Si hubieran añadido un axioma más para la activación, como en la vida
real, y hubieran tenido en cuenta un límite máximo, se podría simular
un circuito xor con la misma cantidad de neuronas. Por ejemplo,
suponiendo que el límite inferior es 25 y el superior es 100, el
circuito podría ser:
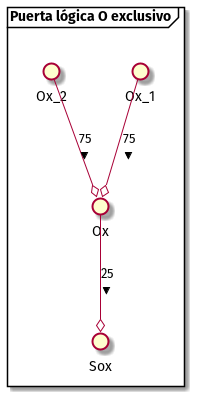
| \(Ox_1\) | \(Ox_2\) | \(Ox\) | |
|---|---|---|---|
| 75 | 75 | 150 | no activa |
| 75 | 0 | 75 | Activa |
| 0 | 75 | 75 | Activa |
| 0 | 0 | 0 | no activa |
¿Por qué esto es importante?
Pues todo tiene que ver con la economía de recursos. Una puerta lógica
debería funcionar de manera directa sin necesitar recursos adicionales
para ello. En este caso necesita una neurona adicional. No sólo eso,
sino que además tiene que ver con el encadenado de puertas lógicas.
Hay bastante más puertas lógicas y dejadme que haga un poco de
hincapié en alguna de ella. En concreto hay una puerta lógica que en
inglés se llama NotXor (¿de qué me sonará el nombre?) que se la
conoce como el lógico universal. Es decir, podemos crear todas las
demás puertas lógicas encadenando sólo puertas notxor, lo que viene
a decir que seríamos capaces de crear cualquier tipo de circuito
lógico sólo con un cajón cargado de «sienes y sienes» de pichorros
de mi puerta lógica favorita.
Otras neuronas y redes neuronales
Más allá de McCulloch y Pitts aparecieron otros modelos intentando mejorar el original. En 1943 la propuesta de estos autores se basaban en lo que se conoce como la lógica del umbral, pero, como hemos visto, ésta se quedaba corta. Además no existía forma alguna de enseñar o entrenar a nuestra red: había que programarle los pesos a puro huevo, como he hecho yo en los ejemplos anteriores. Nada complicado cuanto tienes tres neuronas, pero por cada neurona que añadas la complejidad crece exponencialmente.
Así aparecieron pronto otras soluciones, no sobre las neuronas artificiales en sí, sino sobre cómo reunirlas en redes y capas para que hagan su trabajo. Pero principalmente, sobre el entrenamiento de dichas redes.
Por aquellos años lo petaba un psicólogo (Donald Hebb5) cuyas teorías, que él llamó biopsicológicas, basaban el comportamiento de aprendizaje humano en la plasticidad de las neuronas. En la capacidad que tienen para hacer nuevas sinapsis o en dejar de hacerlas. Esa plasticidad hace, según el autor, que las neuronas establezcan redes de potenciación a largo plazo que está en la base de lo que para las redes neuronales artificiales se conoce como aprendizaje no supervisado... pero me estoy adelantando un poco, voy a seguir un rato más con las redes neuronales, luego ya veremos un poco el tema del aprendizaje.
Históricamente podemos distinguir dos tipos de redes:
- Redes de propagación hacia adelante o redes neuronales prealimentadas que consiste en que las neuronas se agrupan en capas y se comunican hacia adelante en las capas, desde la entrada a la salida conectándose siempre de una capa a la siguiente sin conectar su axón con ninguna anterior. El ejemplo, más sencillo de este tipo de redes es el perceptrón de dos capas, una capa de entrada y otra de salida.
- Redes de estado estocástico, como las redes de Hopfield o la máquina de Boltzmann. Estas redes contienen un conjunto de neuronas completamente interconectadas y que introducen el concepto de estados de mínima energía.
Básicamente, las primeras procesan y las segundas almacenan estados6. Esas son además los tipos de redes neuronales tradicionales e históricas. Sin embargo, en la actualidad hay más:
- Las redes neuronales de impulsos son redes neuronales más modernas que intentan procesar la información de una manera más similar a como lo hacen las redes neuronales biológicas.
Como se puede ver, hay varios tipos de redes y a veces es complicado catalogar una determinada en un grupo o en otro, sin contar los casos de utilizar dos tipos de redes conectados entre ellas para que una le sirva a otra como entrada o como almacenamiento de información. Hay otro tipo de redes que se llaman «recursivas» que almacenan respuestas intermedias que luego se emplean también en la entrada, que me voy a saltar para no marear más la perdiz.
Otros tipos de Inteligencia Artificial
El problema de las redes neuronales en la historia, es la manera en la que aprenden. De hecho, históricamente se abandonaron en favor de otros tipos de Inteligencia Artificial por la dificultad de adiestrar o entrenar a la red para que hiciera lo que se esperaba de ella.
Cuando hace unos años hicimos un intento de crear una red neuronal en Python, el amigo dddddd y yo nos encontramos con esa misma dificultad. Habíamos cambiado el modo en que funcionaba la red neuronal y nos tropezamos con que los métodos clásicos no se ajustaban a nuestra red (o nuestra red a esos métodos) y al final el proyecto quedó abandonado por falta de algoritmo de entrenamiento efectivo.
Así, los modelos llamados entonces sistemas expertos tomaron la
delantera, adquirieron más inversión y más presencia en las
universidades y publicaciones científicas. LISP apareció como el
paradigma de lenguaje de programación para IA, pues el mismo código,
a base de listas, es en sí una base de datos y esa base de datos de
conocimiento, al final, es código LISP. Pero como esas cosas son más
carne de cañón para otros artículos, y este va de redes neuronales, lo
dejaremos para más adelante como otro posible tema para el blog. Ya me
perdonaréis las disculpas.
Métodos de entrenamiento
Ocurrió que se inventó el método de propagación hacia atrás y el conexionismo reapareció de nuevo en el campo de la IA arrollando todo de nuevo a su paso. El método mencionado consiste en comparar el resultado de nuestra red, ─típicamente un perceptrón multicapa─, con el resultado esperado. Si el valor no coincide y/o se distancia de lo esperado, se modifican los pesos de las sinapsis siguiendo las capas hacia atrás y volviendo a probar.
Contado así es fácil de entender cómo funciona. Otro tema es implementarlo, que es bastante más complejo.
Otra forma en realidad no es un método de entrenamiento, es la utilización de algoritmos evolutivos, aprovechando que al final la selección natural no deja de ser un buen mecanismo para producir determinados resultados si conoces cuáles son los que buscas. También se les conocen como métodos aleatorios, pues modifican los pesos al azar y se van seleccionado aquellas modificaciones que se aproximan más al resultado esperado, para repetir el proceso en sucesivas generaciones, hasta alcanzar la salida deseada.
Conclusiones
Bueno, esto es sólo arañar un poco la superficie del tema de las redes neuronales, ─y eso sin profundizar mucho en las redes modernas y el Big Data... uff─, un tema apasionante, pero muy complejo para verlo completamente en un sólo artículo. Tampoco soy un experto, sólo soy un curioso y las cosas que digo son las que creo saber. Espero no estar muy errado en el fondo de la cuestión.
Estoy pensando ampliar el tema un poco y meterle algo de programación
al tema... pero como no sé qué pensarán los sufridos lectores de mis
tontás esperaré a los comentarios por redes sociales. Si os apetece,
lo mismo hago una serie sobre programar una red neuronal y practicar
lo poco que sé de erlang/OTP por el camino.
Footnotes:
Era la forma de la época pre-informatizada para que los profesores nos dejaran documentos a los alumnos... los llevaban a repografía y luego tú comprabas allí las fotocopias. Muchas veces, como ésta, eran los borradores de libros escritos preparados para publicar.
El Curso de Orientación Universitaria de entonces, o un curso que se supone que te preparaba para la Universidad.
Fíjese el respetable que no es neurona artificial, sino formal: está expresada mediante axiomas matemáticos ya que en 1943 no había mucha posibilidad de programar una artificial.
Este es un planteamiento irreal, pues las neuronas naturales hacen sinapsis sobre sí mismas, pero lo dejaremos estar.
No me cayó nunca muy bien: lideró los estudios sobre privación sensorial que luego aparecerían aplicados en los manuales de tortura de la CIA.
Como esto lo lea un entendido de verdad se va a descojonar de todas las burradas que puedo decir en aras de la simplificación... pero para el caso nos sirve.


Comentarios