Un Morph reloj (El libro de Cuis-Smalltalk)

Siguiente: Volviendo a los Morphs de Spacewar!, Anterior: Pasando a Vector, Arriba: Los fundamentos de Morph [Índice general][Índice]

7.2 Un Morph reloj ¶

Con todo lo que ya hemos aprendido, podemos crear un morph más sofisticado. Creemos un ClockMorph como se ve en la Figura 7.5.

Figura 7.5: Un morph reloj

Creemos ClockMorph, el reloj de esfera:

PlacedMorph subclass: #ClockMorph
   instanceVariableNames: ''
   classVariableNames: ''
   poolDictionaries: ''
   category: 'Morphic-Learning'

...y su método de dibujo en la categoría drawing:

ClockMorph>>drawOn: aCanvas
   aCanvas
      ellipseCenter: 0@0
      radius: 100
      borderWidth: 10
      borderColor: Color lightCyan
      fillColor: Color veryVeryLightGray.
   aCanvas drawString: 'XII' at: -13 @ -90 font: nil color: Color brown.
   aCanvas drawString: 'III' at: 66 @ -10 font: nil color: Color brown.
   aCanvas drawString: 'VI' at: -11 @ 70 font: nil color: Color brown.
   aCanvas drawString: 'IX' at: -90 @ -10 font: nil color: Color brown

Ejemplo 7.2: Dibujando el reloj de esfera

Creamos ClockHourHandMorph, la manecilla para las horas:

PlacedMorph subclass: #ClockHourHandMorph
   instanceVariableNames: ''
   classVariableNames: ''
   poolDictionaries: ''
   category: 'Morphic-Learning'

...y su método de dibujado en la categoría drawing:

ClockHourHandMorph>>drawOn: aCanvas
   aCanvas fillColor: (Color black alpha: 0.6) do: [
      aCanvas
         moveTo: 0 @ 10;
         lineTo: -5 @ 0;
         lineTo: 0 @ -50;
         lineTo: 5 @ 0;
         lineTo: 0 @ 10 ].

Ya puedes empezar a jugar con ellos. Podríamos usar varias instancias de un único ClockHandMorph, o crear varias clases. Aquí hemos optado por lo segundo. Ten en cuenta que todos los métodos drawOn: utilizan constantes codificadas para todas las coordenadas. Como hemos visto anteriormente, esto no es una limitación. ¡No necesitamos escribir un montón de fórmulas trigonométricas y de escalado especializadas para crear Morphs en Cuis-Smalltalk!

A estas alturas, quizá ya te imagines lo que estamos haciendo con todo esto, pero ten paciencia mientras terminamos de construir nuestro reloj.

Creamos ClockMinuteHandMorph, la manecilla de los minutos:

PlacedMorph subclass: #ClockMinuteHandMorph
   instanceVariableNames: ''
   classVariableNames: ''
   poolDictionaries: ''
   category: 'Morphic-Learning'

...y su método de dibujado en la categoría drawing:

ClockMinuteHandMorph>>drawOn: aCanvas
   aCanvas fillColor: ((Color black) alpha: 0.6) do: [
      aCanvas
         moveTo: 0 @ 8;
         lineTo: -4 @ 0;
         lineTo: 0 @ -82;
         lineTo: 4 @ 0;
         lineTo: 0 @ 8 ]

Y por último, la ClockSecondHandMorph, la manecilla de los segundos:

PlacedMorph subclass: #ClockSecondHandMorph
   instanceVariableNames: ''
   classVariableNames: ''
   poolDictionaries: ''
   category: 'Morphic-Learning'

...y su método de dibujado en la categoría drawing:

ClockSecondHandMorph>>drawOn: aCanvas
   aCanvas strokeWidth: 2.5 color: Color red do: [
      aCanvas
         moveTo: 0 @ 0;
         lineTo: 0 @ -85 ]

Ahora, solo queda juntar las piezas de nuestro reloj en ClockMorph. En su categoría de métodos initialization, añade su método initialize (acepta los nuevos nombres como variables de instancia):

ClockMorph>>initialize
   super initialize.
   self addMorph: (hourHand := ClockHourHandMorph new).
   self addMorph: (minuteHand := ClockMinuteHandMorph new).
   self addMorph: (secondHand := ClockSecondHandMorph new)

Si aún no has añadido variables de instancia para las manecillas del reloj, el IDE Cuis lo detectará y te preguntará qué quieres hacer al respecto. Queremos declarar los tres nombres que faltan como variables de instancia.

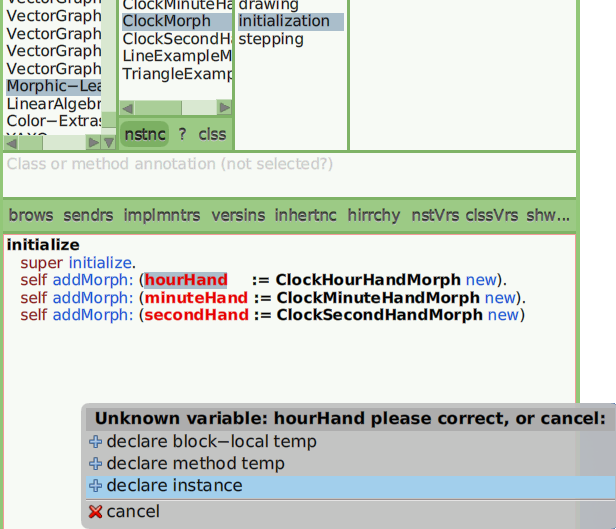
Figura 7.6: Declarar variables desconocidas como variables de instancia en la clase actual

¡La definición de tu clase ClockMorph ya debería estar completa!

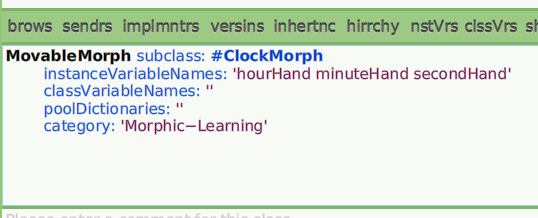
Figura 7.7: ClockMorph con variables de instancia añadidas

Por último, animamos nuestro reloj. En la categoría de métodos stepping, añade el método:

ClockMorph>>wantsSteps
   ^ true

...y:

ClockMorph>>step
   | time |
   time := Time now.
   hourHand rotationDegrees: time hour * 30.
   minuteHand rotationDegrees: time minute * 6.
   secondHand rotationDegrees: time second * 6

Echa un vistazo a cómo actualizamos las manecillas del reloj.

Como dijimos anteriormente, cualquier PlacedMorph define un sistema de coordenadas para su propio método drawOn: y también para sus submorfos. Este nuevo sistema de coordenadas podría incluir la rotación o reflexión del eje y el escalado de tamaños, pero por defecto no lo hace. Esto significa que solo trasladan el origen, especificando dónde se ubicará el punto propietario 0 @ 0.

El sistema de coordenadas del World tiene 0 @ 0 en la esquina superior izquierda, con las coordenadas X aumentando hacia la derecha y las coordenadas Y aumentando hacia abajo. Las rotaciones positivas van en el sentido de las agujas del reloj. Esta es la convención habitual en los marcos gráficos. Tenga en cuenta que esto difiere de la convención matemática habitual, en la que Y aumenta hacia arriba y los ángulos positivos van en sentido contrario a las agujas del reloj.

Entonces, ¿cómo actualizamos las manecillas? Por ejemplo, para la manecilla de las horas, una hora significa 30 grados, ya que 12 horas significan 360 grados o una vuelta completa. Por lo tanto, multiplicamos las horas por 30 para obtener los grados. Las manecillas de los minutos y los segundos funcionan de manera similar, pero como hay 60 minutos en una hora y 60 segundos en un minuto, debemos multiplicarlos por 6 para obtener los grados. Como la rotación se realiza alrededor del origen, y el reloj ha establecido el origen en su centro (Ejemplo 7.2), no es necesario establecer la posición de las manecillas. Por lo tanto, su origen 0 @ 0 estará en el reloj 0 @ 0, es decir, en el centro del reloj.

Figura 7.8: Un elegante morph de reloj

Mira el reloj de la Figura 7.8. ¿No te parece elegante la manecilla de los segundos decorada con un disco rojo y amarillo? ¿Cómo modificarías nuestro morph de reloj para obtener este resultado?

Ejercicio 7.3: Un reloj elegante

Crea algunas instancias de tu reloj: ClockMorph new openInWorld. Puedes girarlo y ampliarlo. Fíjate en la calidad visual de los números romanos de la esfera del reloj, especialmente cuando se gira y se amplía. ¡No obtendrás esta calidad gráfica en tu entorno de programación habitual! También puedes extraer las partes o escalarlas por separado. Otro experimento divertido consiste en extraer los números romanos a un ClockFaceMorph independiente y convertirlo en un submorph del reloj. A continuación, puedes girar solo la esfera, no el reloj, y este mostrará una hora falsa. ¡Pruébalo!

Sin embargo, es posible que hayas notado que faltan dos cosas: cómo calcular los rectángulos delimitadores para los Morphs y cómo detectar si un Morph está siendo tocado por el cursor, para poder moverlo u obtener un halo. El rectángulo de visualización que contiene completamente un morph es necesario para que el marco gestione la actualización requerida de las áreas de visualización como resultado de cualquier cambio. Pero no es necesario conocer este rectángulo para crear tus propios Morphs. En Cuis-Smalltalk, el marco lo calcula según sea necesario y lo almacena en la variable privateDisplayBounds. No tienes que preocuparte en absoluto por esa variable.

Con respecto a detectar si el cursor está tocando un Morph o, en términos más generales, si algún píxel pertenece a un Morph, lo cierto es que durante la operación de dibujo de un Morph, el marco conoce todos los píxeles a los que afecta. El método drawOn: especifica completamente la forma del Morph. Por lo tanto, no es necesario pedir al programador que vuelva a codificar la geometría del Morph en un método separado. Lo único que se necesita es un diseño cuidadoso del propio marco, para evitar que los programadores tengan que lidiar con esta complejidad adicional.

Las ideas que hemos esbozado en este capítulo son las fundamentales en Morphic, y el marco se implementa con el fin de respaldarlas. Los morphs (es decir, los objetos gráficos interactivos) son muy generales y flexibles. No se limitan a una biblioteca de widgets convencional, aunque se incluye una biblioteca de este tipo (basada en BoxedMorph) que se utiliza para crear todas las herramientas de Smalltalk.

Los ejemplos que hemos explorado utilizan el marco VectorGraphics. Incluye las clases VectorCanvas y HybridCanvas. Cuis-Smalltalk también incluye la clase heredada BitBltCanvas, heredada de Squeak. BitBltCanvas no admite las operaciones de dibujo de gráficos vectoriales y no realiza suavizado ni zoom. Sin embargo, es madura y se basa en la operación BitBlt incluida en la VM. Esto significa que ofrece un rendimiento excelente.

Para explorar más a fondo Morphic de Cuis-Smalltalk, evalúe Feature require: 'SVG' y, a continuación, SVGMainMorph exampleLion openInWorld y los demás ejemplos que hay allí. Además, asegúrese de probar los ejemplos de la categoría de clase Morphic-Examples, entre ellos, ejecute Sample10PythagorasTree new openInWorld y juegue con las direcciones arriba y abajo, izquierda y derecha de la rueda del ratón.

Antes de dejar esta sección, aquí hay un cambio de dos líneas para convertir nuestro reloj de cuarzo Cuis²⁴ en un reloj suizo automático²⁵ ²⁶:

ClockMorph>>stepTime
    ^ 100 "milliseconds"
ClockMorph>>step
../..
   secondHand rotationDegrees: (time second + (time nanoSecond * 1.0e-9))* 6

Intenta comprender cómo afectan estos cambios al comportamiento del segundero y en qué fracción de segundo gira.

7.2 Un Morph reloj ¶

Notas al pie

(24)

(25)

(26)